Lecture 03: Transformation

二维变换
缩放变换

用矩阵表示,矩阵就叫缩放矩阵
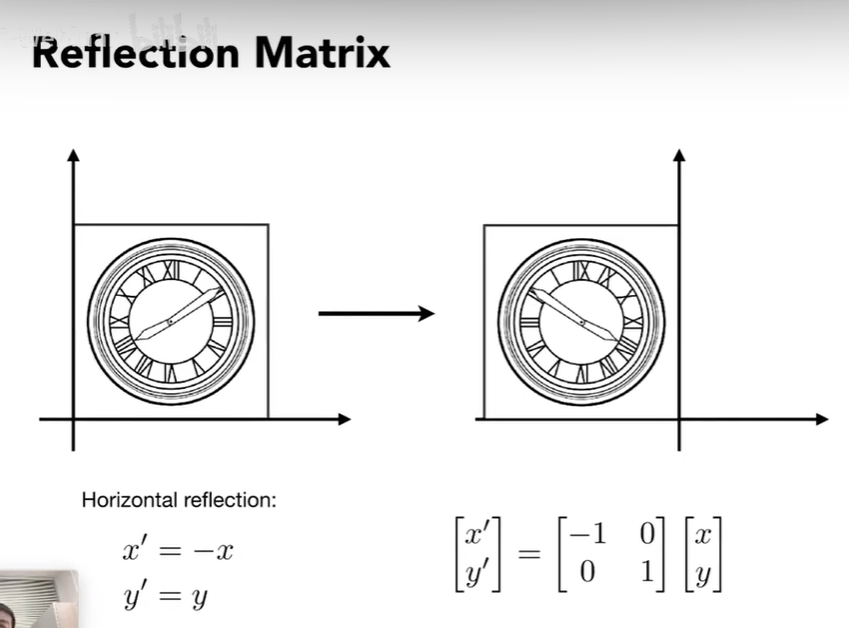
对称变换一下:
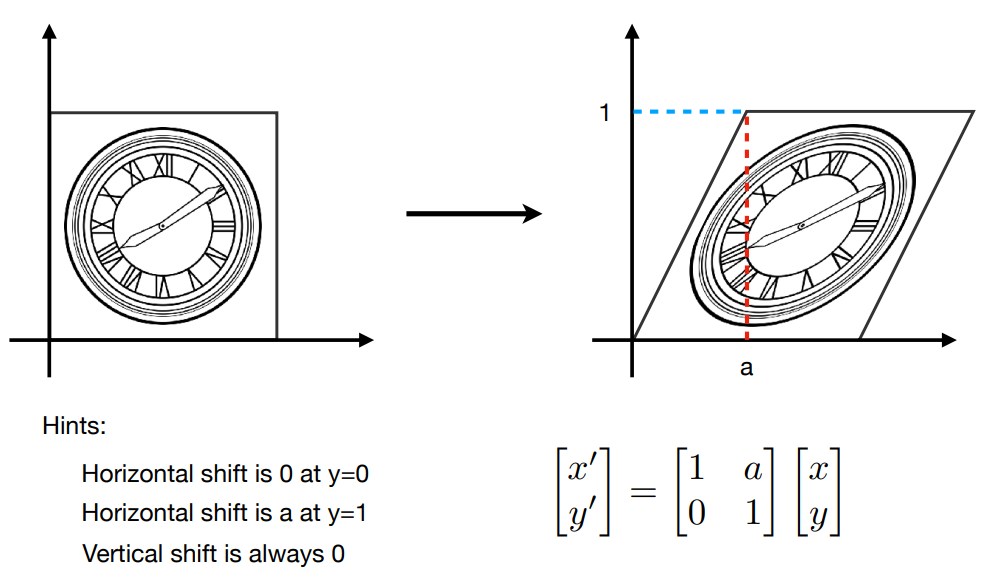
复杂一点的:
这里的 x 的变换 和 y 是有关系的 x’ = x + ay
旋转变换
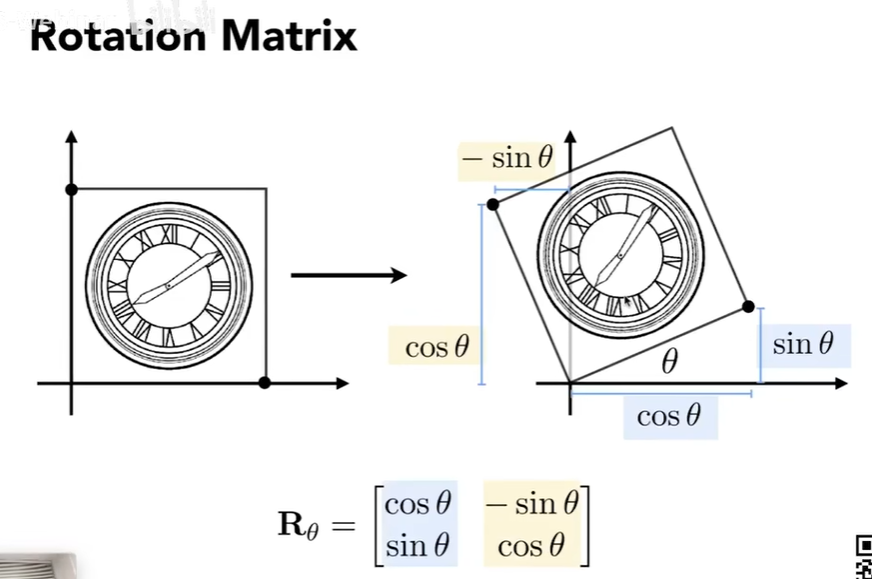
推导:
推关系(x’ 和 x)(y’ 和 y):(利用特殊点(1,0))
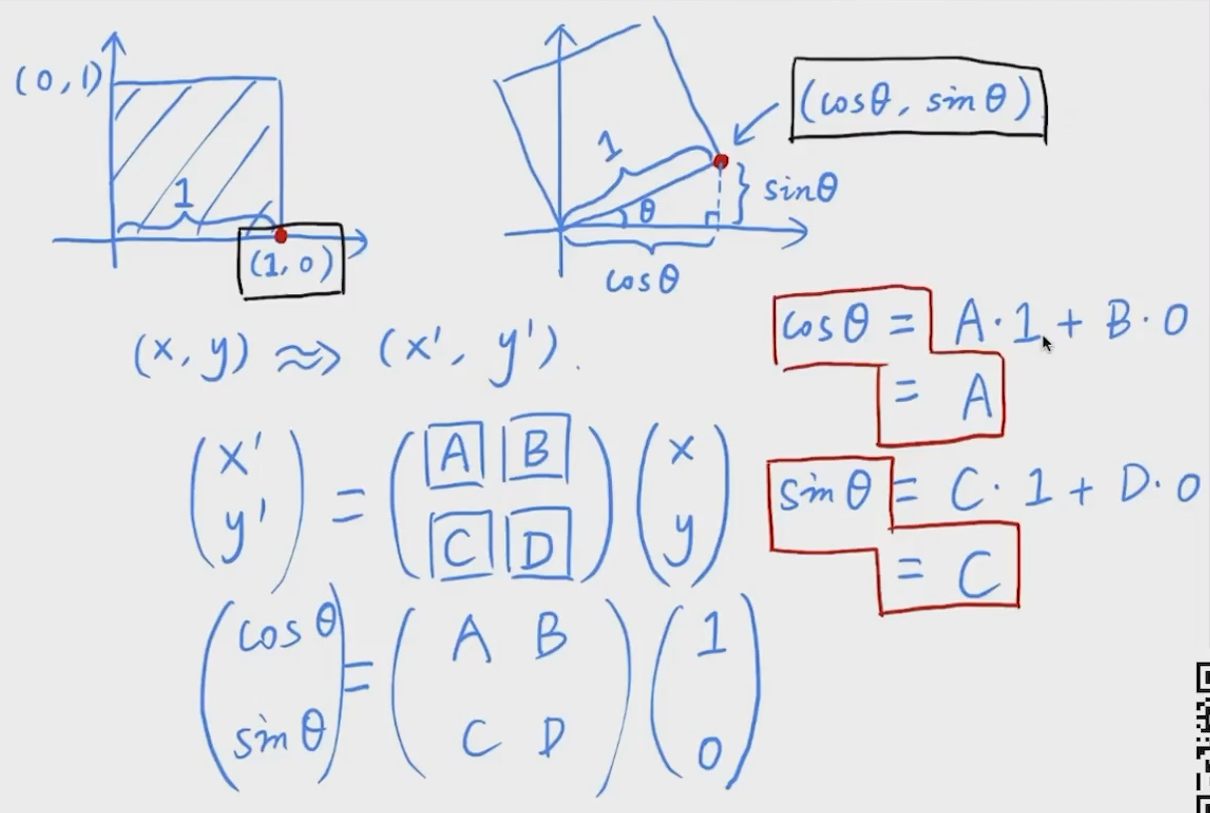
从上图可以得到:
A = cosθ
C = sinθ
同理,用特殊点(0,1)算出B D
B = -sinθ
D = cosθ
所以可以得到旋转矩阵 Rθ;
记忆:
记图,然后自己推到一下就行!
性质:
旋转矩阵的转置 <=> 旋转矩阵的逆
如果一个 矩阵转置 = 矩阵的逆,则这个矩阵叫做正交矩阵
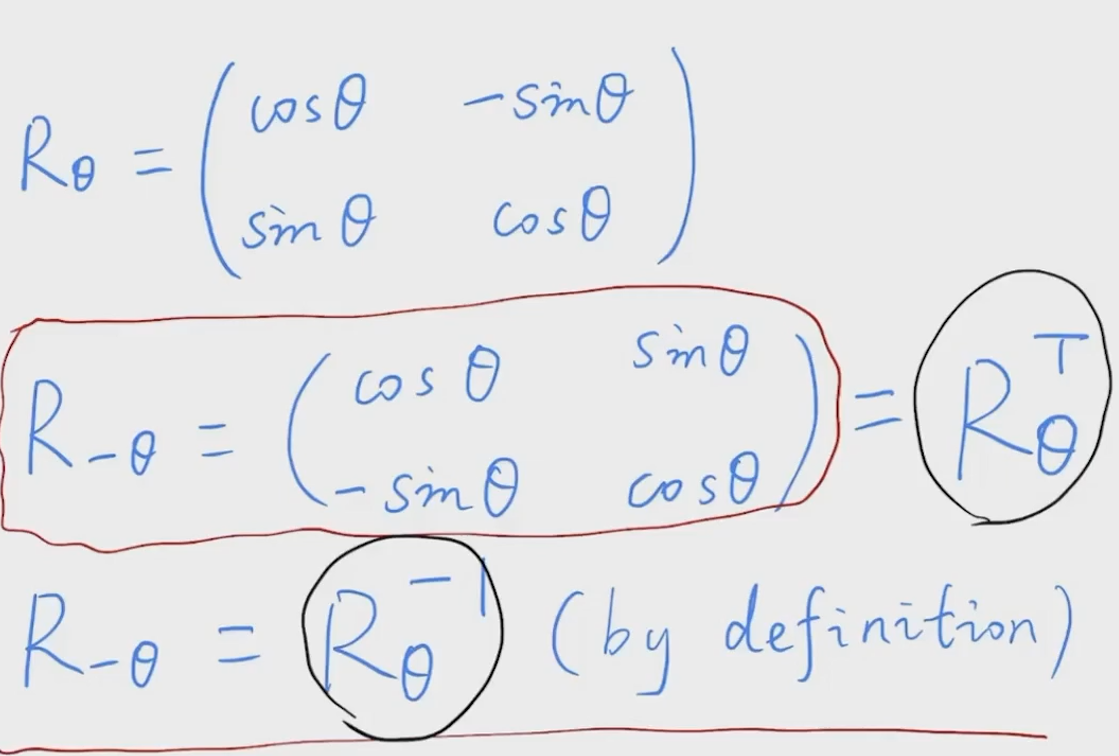
小结
线性变换:输入坐标 * 矩阵 = 输出坐标
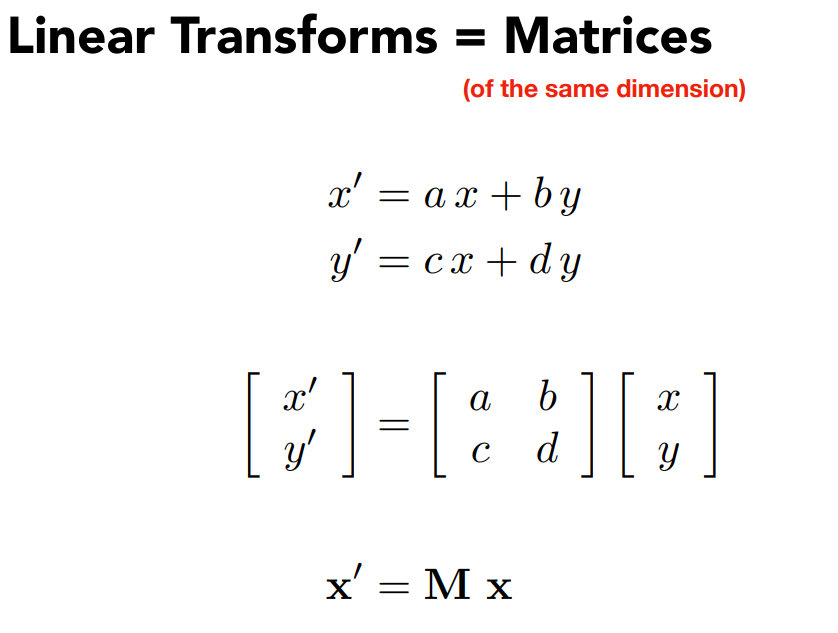
上面的例子统称为线性变换
齐次坐标(统一变换)
为什么?
当我们平移图像的时候,可以发现我们无法用之前的简单的矩阵x向量的形式表示,而是得用下面的表示方法:
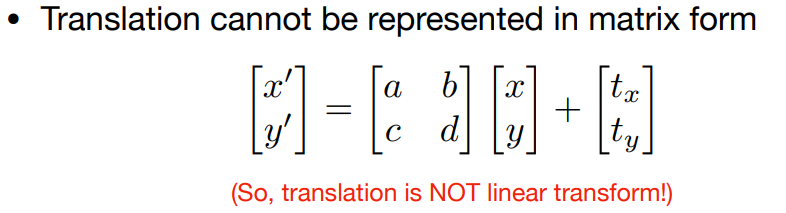
所以,平移不属于线性变换;
但是我们不想要它特殊,所以引入了齐次坐标,用于表示各种变换!
怎么做?
首先,用三个数来表示一个二维向量;
相当于就是把二维变成三维,然后用特殊的数字去表示三维!
- 点:第三维是 1
- 向量:第三维是 0
这样就能通过齐次坐标的方式,把所有的变换都表示成 矩阵 x 向量 的形式;

为什么向量第三维是 0 ?
这么做是为了保证向量的平移不变性;
同时保证了在一些运算下仍然是正确的;
在齐次坐标下:point1 + point2 = point 1 2 的中点

(x1,y1,w)转置 + (x2,y2,w)转置
=> ( (x1+x2) , (y1+y2) , 2w )转置
=> ( (x1+x2)/2w , (y1+y2)/2w , 1)
小结
仿射变换:
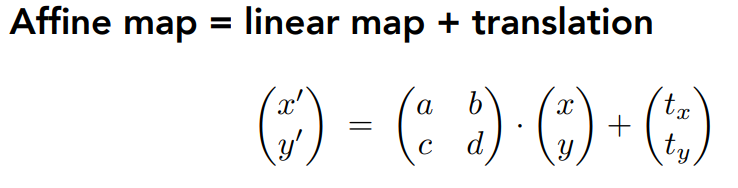
齐次变换:
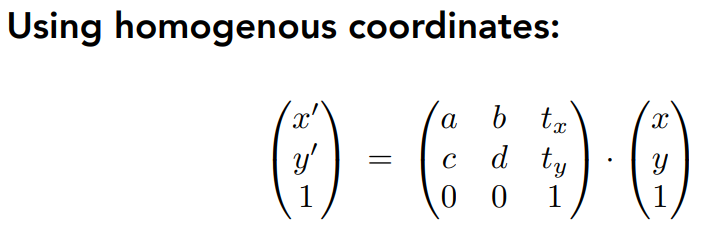
注意到,在表示二维坐标的仿射变换中,齐次变换矩阵的最后一行都是(0,0,1);
注意是有条件的,二维坐标,仿射变换.
验证:(缩放,旋转,平移)

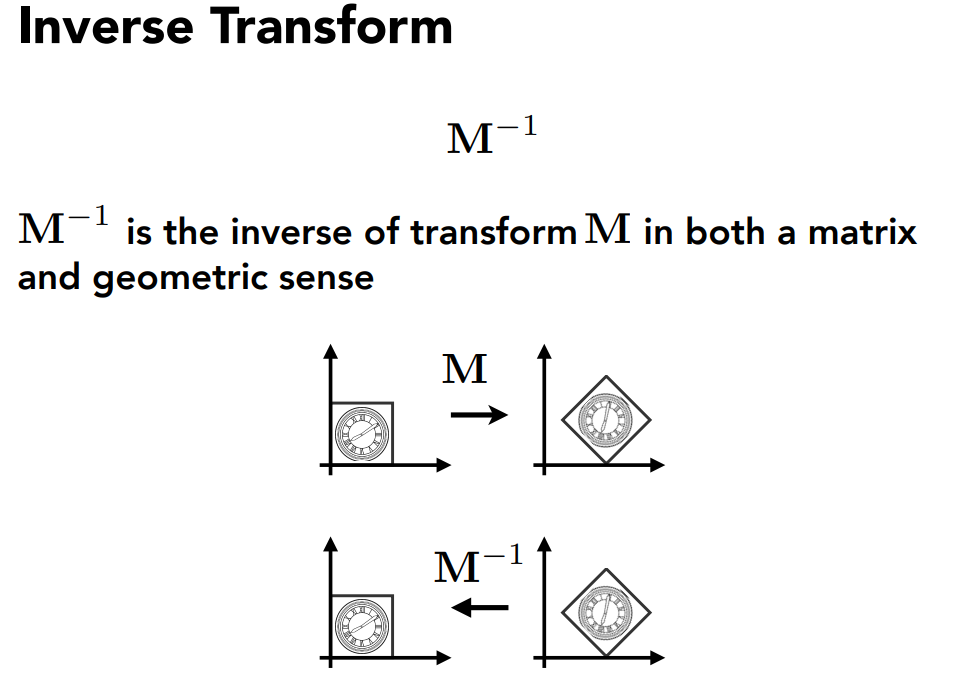
逆变换
要变换回来,则乘以变换矩阵的逆矩阵
变换组合
首先规定,这里默认的旋转是 以0,0为中心,逆时针 旋转的;
变换的顺序很重要;
变换组合 其实本质上就是对应着 矩阵的乘法!!!
当矩阵乘法的顺序不同,得到的变换结果也是不同的。
举个例子:
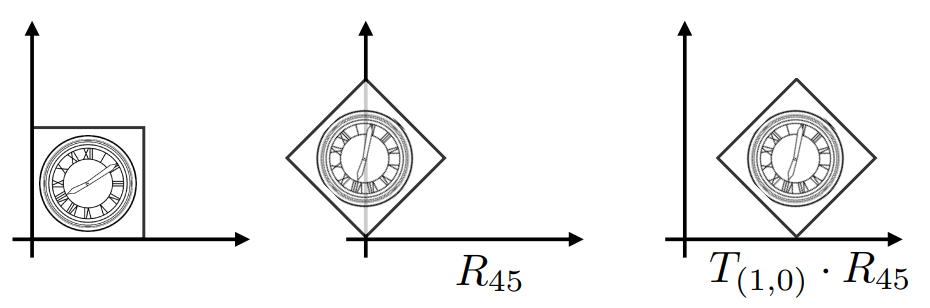
在这个变换中,我们需要先旋转45度,再平移;
那么对应的数学结果就是:
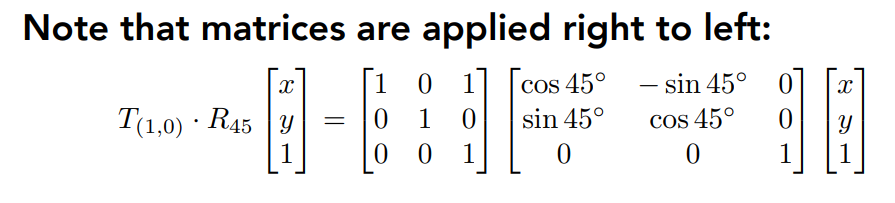
总结:
我们按照变换的顺序,在原向量的基础上,往原向量的左边,从右往左依次乘上变换矩阵

值得注意的是:矩阵乘法有结合律!
变换的分解
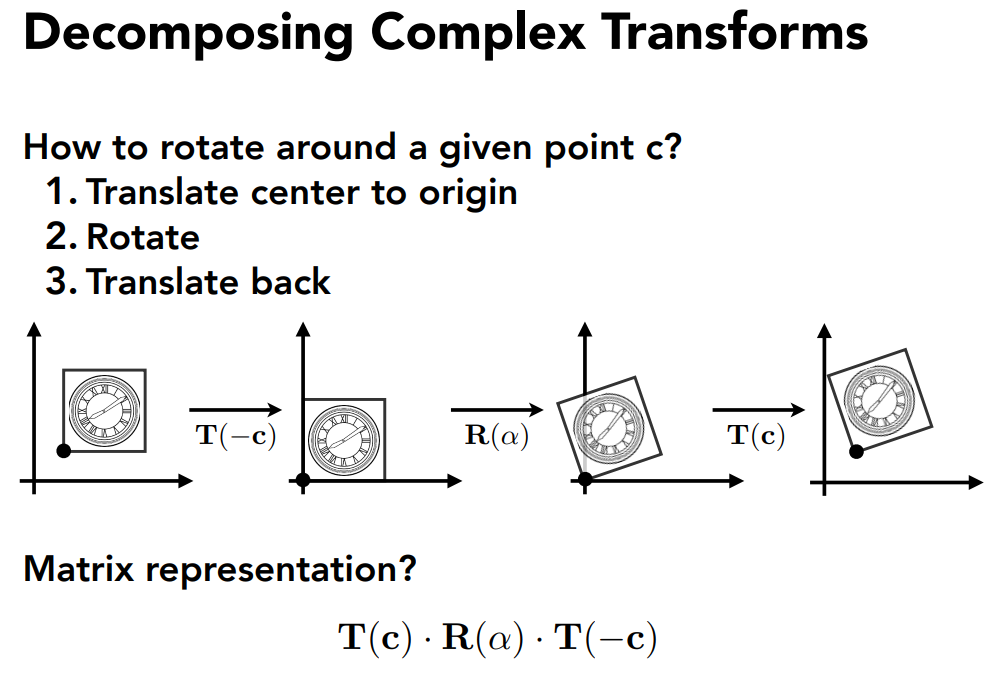
三维变换
同理,在三维变换中,也有平移这样的非线性变换操作;
所以继续引入齐次坐标;
用四个数去表示三维空间;
三维变成四维,第四维度取特殊值;
- 描述点,最后一维为1;
- 描述向量,最后一维为0;

当 w != 0 时,齐次坐标下的点 (x , y, z , w) , 则表示三维空间中的点 (x/w , y/w , z/w)
将 x y z 都 /w 就可以表示成三维空间中的点了!
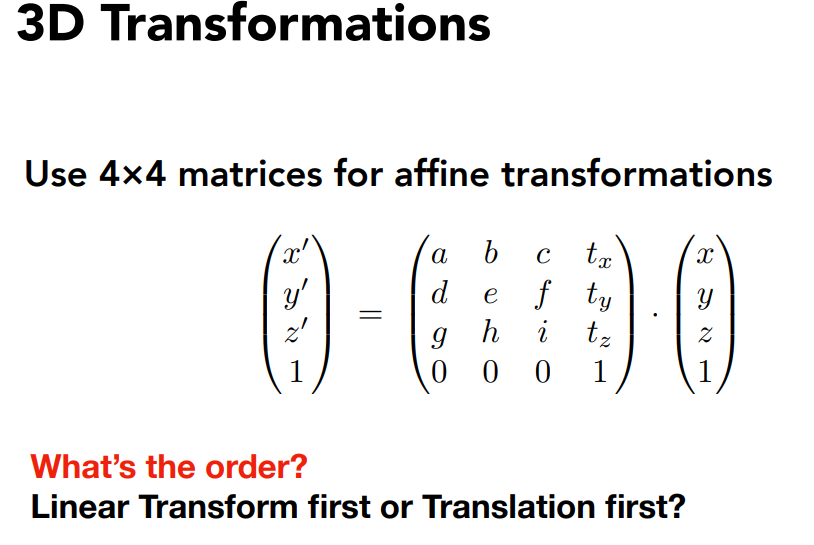
同样的,在描述三维空间中的反射变换时,变换矩阵的最后一行是(0,0,0,1);
平移操作还是体现在最后一列;
值得注意的是 :
当我们写出齐次坐标的时候,它表示的其实是:
先线性变换,在进行平移!
具体的变换 :
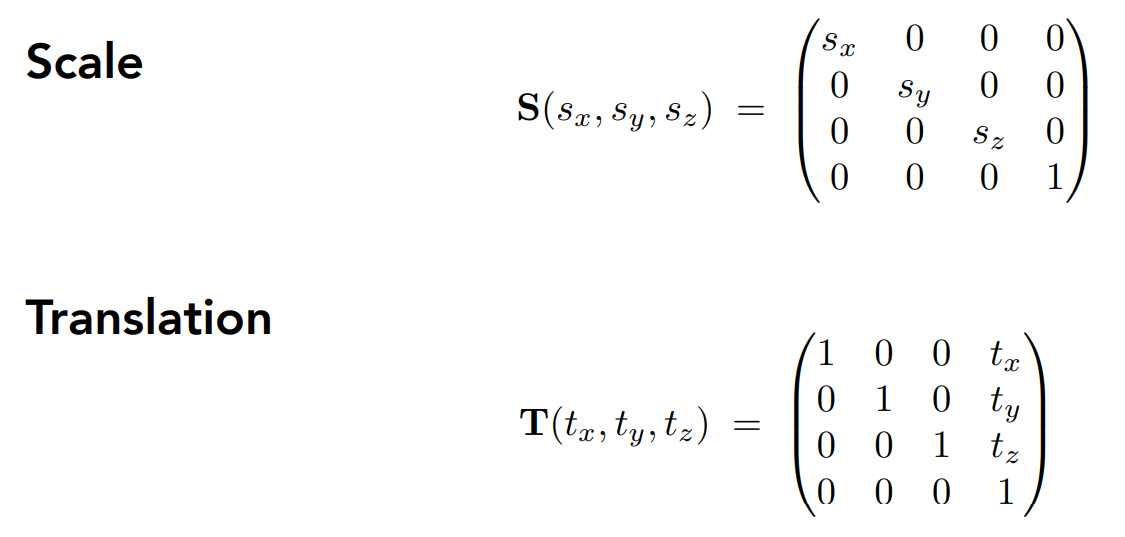
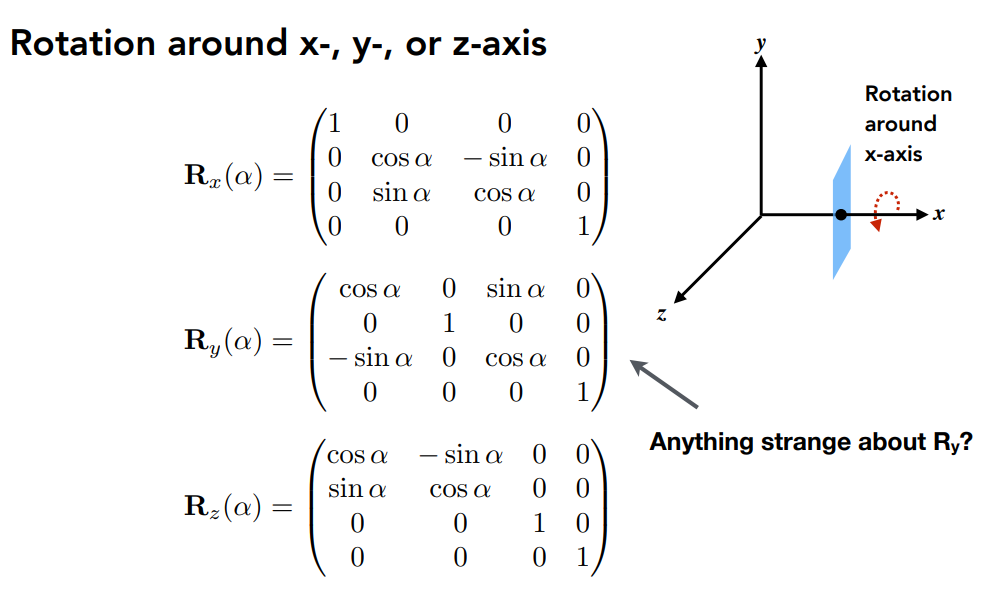
这里注意一下绕y轴为啥是反的?这个和轴的顺序和右手螺旋定则有关;
补充
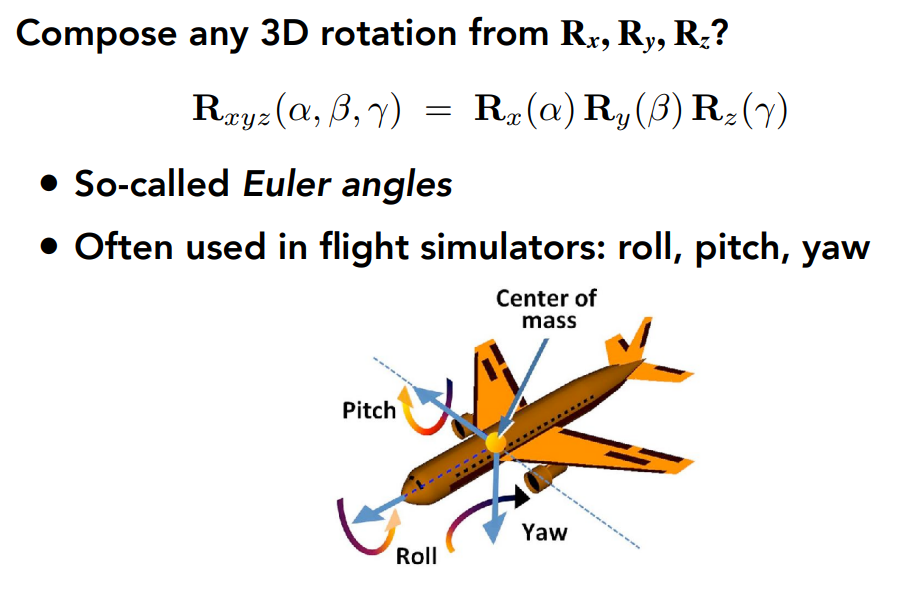
任意一个3D的旋转,都可以分解为分别绕x y z轴旋转;
a β γ 称为欧拉角
Rodrigues’ 旋转公式:
就是能把任意一个旋转分解为绕 x y z 的旋转:

n向量:旋转轴(可以理解为一个方向向量,且规定n过原点)
a:旋转角度
推导:
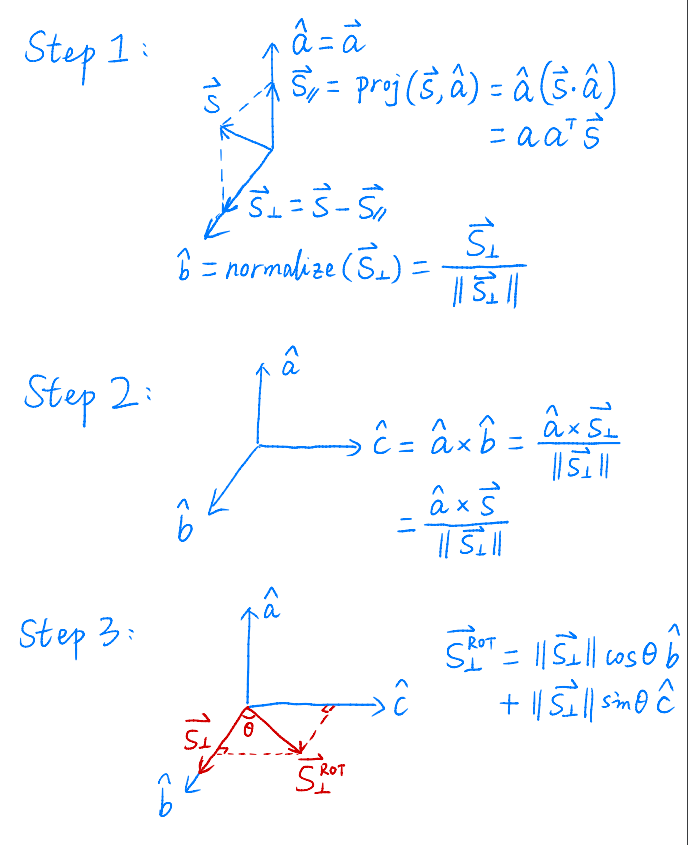
扩展 :
四元数 : 主要用于两个旋转之间的插值