Lecture 04 : Transformation Cont.
概述

View / Camera transformation:视图变换 / 相机变换
Projection transformation:投影变换
图形学:正交/透视投影矩阵的推导(多个思路) - 知乎 (zhihu.com)
上面这一边里面讲的非常清楚了 !
视图变换
试图变换是什么?
三元素 :
- 把场景搭好(model transformation,模型变换)
- 找一个好的角度,把相机放好(view transformation,视图变换)
- 然后拍照(projection transformation,投影变换)
简称 MVP 变换
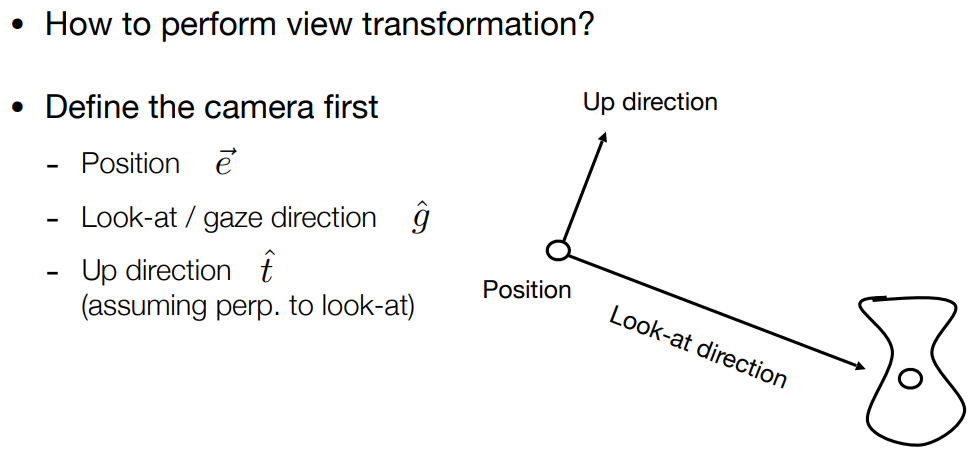
特别解释 :
- 位置:这个没啥好说的…就是一个坐标
- 凝视方向:也就是向哪里看,这里其实包含了两个方向,我们把头当作摄像机,那么凝视方向就包含了我们头左右看和上下看的元素(不歪头)
- 向上方向:这个不是说向上看的意思…还是把我们的头当作摄像机,当我们确定了头的位置和凝视方向时,当我们歪头时,我们可以发现我们看到的还是不同的,所以我们还需要一个元素来约束;这里引入一个始终垂直于我们头顶的法向量,这个法向量指向的方向就是向上方向,当我们歪头时,这个法向量也不同;
因此,通过上面这3个元素,我们可以唯一确定相机看到的图像!!!
如何进行视图变换?
首先我们将相机定,其他东西都随相机移动;
(固定指的是:相机在0 0 0处,且x向前,y向上,-z向右)
具体操作:(初始相机在e点,看向g,向上是t,g叉乘t对应着x)
- 先平移到 0 0 0
- 将 g 旋转到 -z
- 将 t 旋转到 y
- 最后将 g 叉乘 t 旋转到 x
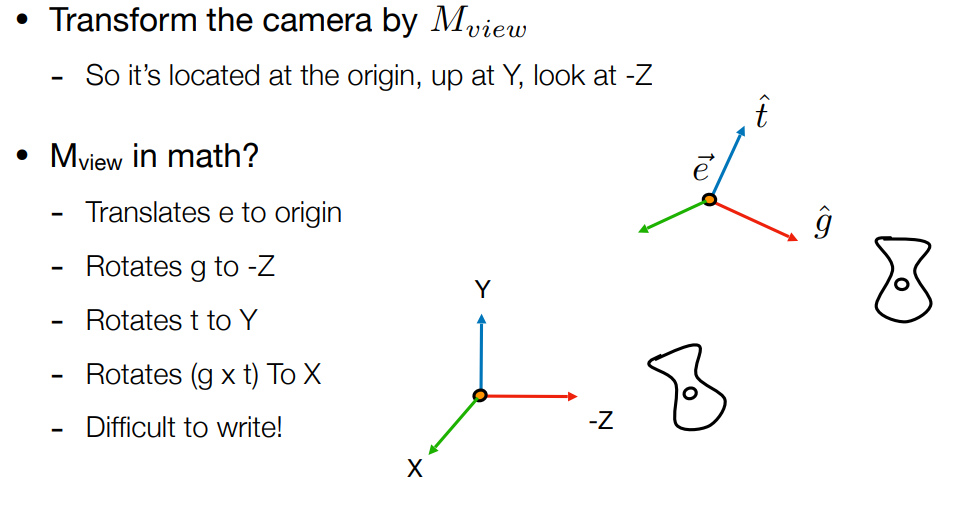
下面是矩阵表示:
直接求这个变换矩阵的话不太好求,我们可以反过来想:
将(x、y、-z)旋转到(g x t、t、g),得到旋转矩阵,将这个旋转矩阵求逆就是我们结果,注意到上节课的性质,这种变换的矩阵是正交矩阵,即 矩阵的逆<=>矩阵的转置,所以直接求矩阵的转置就行。

投影变换
正交投影
无近大远小效果
假设相机在 0 0 0 处,且看向-z方向,向右是x,向上是y;那么将相机x y范围内的的物体的z方向去掉得到的图像就是正交投影
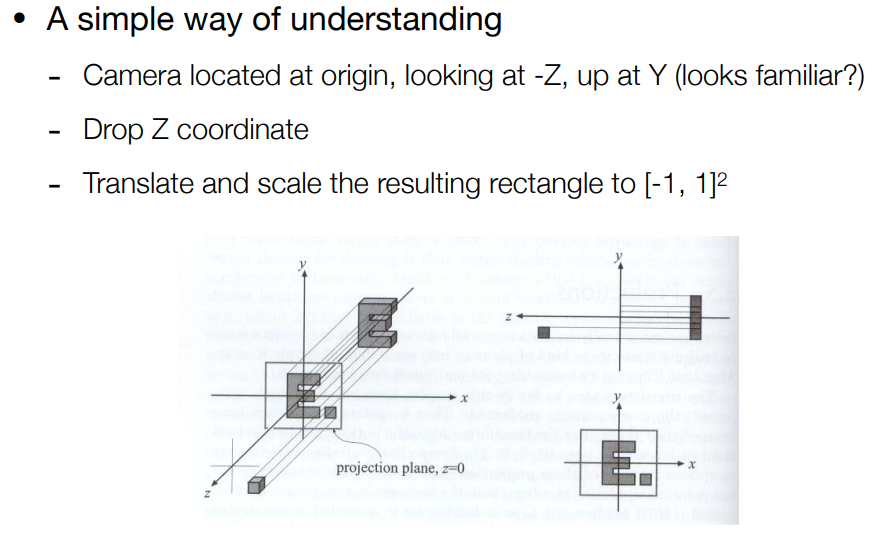
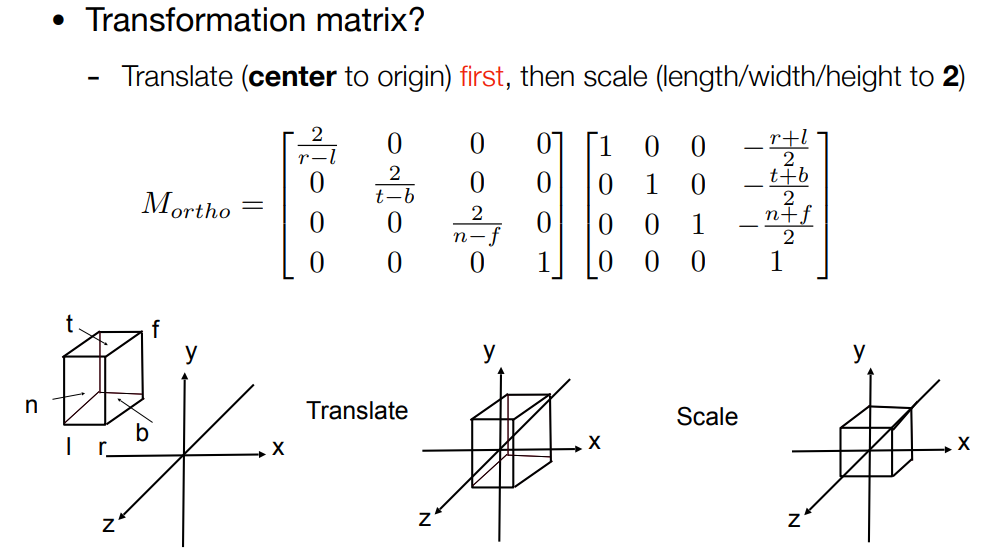
更加规范的:
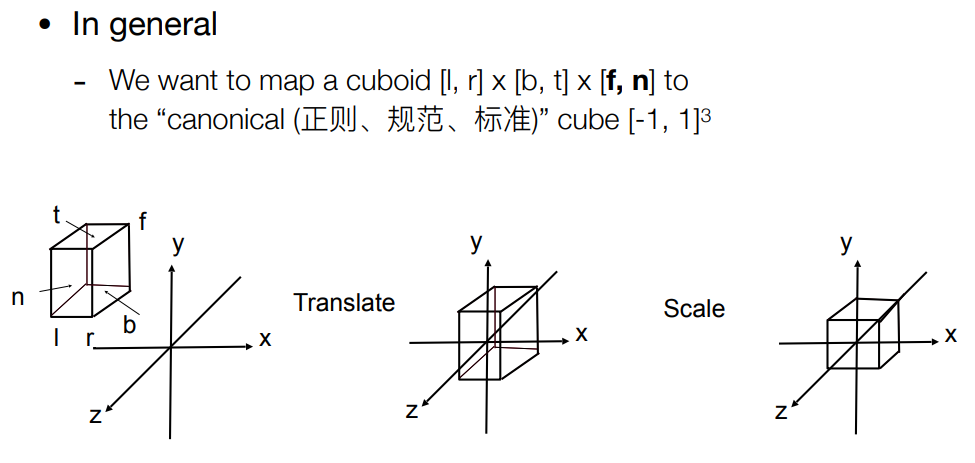
- 先将物体的中心移到原点0 0 0
- 将物体进行缩放,缩放到(-1,1)³的立方体中
(这里长方体等物体会变得不一样… 后面会将再一次拉伸 ( 视口变换 )…)
透视投影
**概述 : **
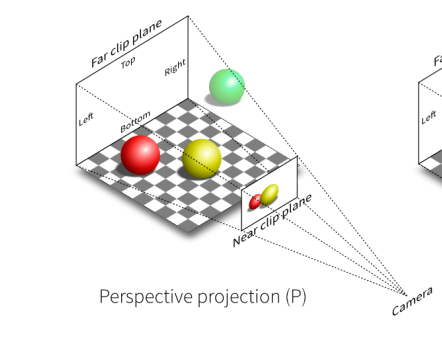
有近大远小效果
回顾一下,前面我们讲了,齐次坐标(用四个数表示三维空间中的 点/向量)

如何进行透视投影?
还是那个问题,正面不好想,我们反着想;
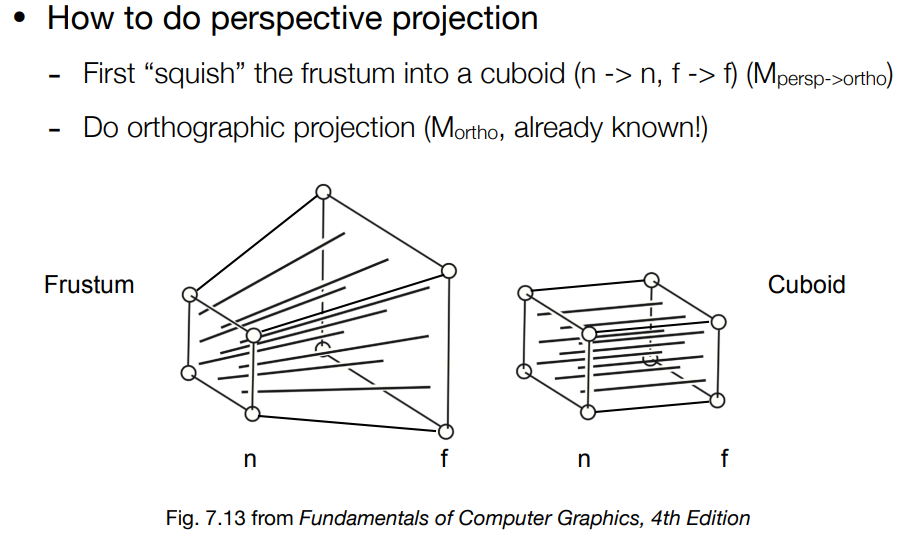
透视投影要做的是将平面变成进平面 ( 挤压 ) ;
也就是如何 透视投影 -> 正交投影,得到变换矩阵之后;求这个变换矩阵的逆,那么这个逆就是 正交投影 -> 透视投影 的结果。
透视投影 -> 正交投影
- 将 透视投影 的梯形体挤压成长方体(近平面不变,远平面挤压,且远平面的z不变,且远平面的中心点的坐标仍然不变)
- 做一遍正交投影
**具体分析 : **
第二步是比较简单的,上面说过了;
下面分析第一步要怎么做???
首先我们要明确一下我们的问题,现在的问题是:
如何将在透视投影中的点(x y z)变换为正交投影中的点(x’ y’ z’),也就是求 透视投影 -> 正交投影 的变换矩阵
首先我们可以发现变换时点在z轴上的变换是比较难求的,这里我们先不考虑z轴的情况,后面再求;
我们先看x轴和y轴的情况,可以发现他们形成一个相似三角形,因此 x’ x,y’ y 的关系很容易就知道了!
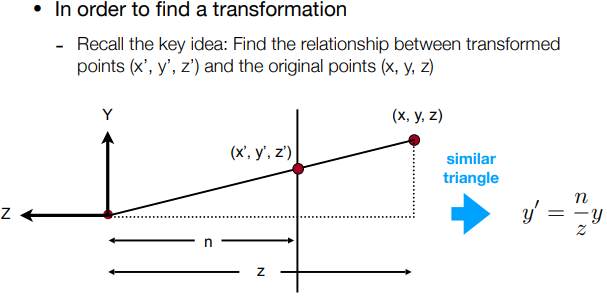

前面说过,齐次坐标下,每个数都同时乘上同一个数,这个点/向量是不变的,表示的还是那个点;所以我们可以进一步的变换:

接着我们试着反推一下这个变换矩阵:(什么样的矩阵 乘上 透视时的点 会变成 正交时的点?)
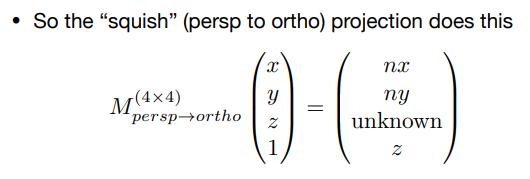
可以发现,我们可以得到这个变换矩阵的大部分信息:
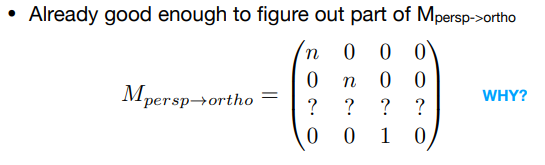
由于我们把这个z轴给展示不管了,所以导致这个变换矩阵的第三行是未知的;现在我们需要通过一些性质去把第三行解出来;可以发现在变换前后有这样两个性质:
- 变换前后,近平面上的点是不变的(x y z都不变);
- 变换前后,远平面上的中心点是不变的(x y z都不变);
我们先利用第一个性质,假设在近平面上有一个点(x y n 1),那么变换之后还是(x y n 1),变换一下为(nx ny n² n);

利用上面的残缺矩阵,我们可知:
(????)(x y n 1)转置 = (nx ny n² n)转置
从而我们可以推出第三行:
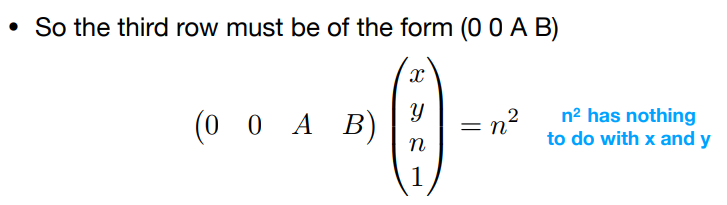
同时得到一个方程:
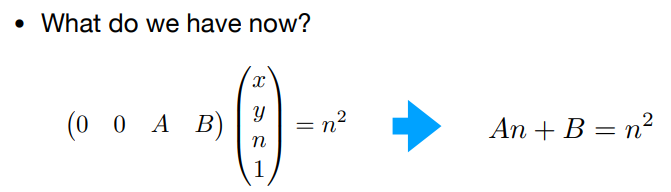
接着我们利用第二个性质:远平面上的中心点为(0 0 f 1),变换后还是(0 0 f 1),同理变换一下(0 0 f² f)
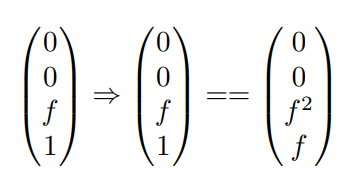
同样,我们可以的到一个方程:

也就是说我们有两个未知数A B,有两个方程,这样就能解除A B,从而得到我们的变换矩阵了!
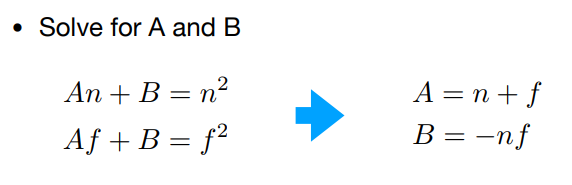
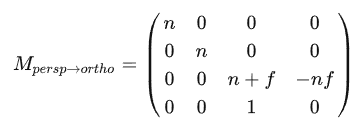
分析结束!!!
注意 :
到这里 , 我们只是求出了 透视投影压缩变换 , 也就是 透视投影 -> 正交投影 ;
所以如果要求透视投影矩阵 , 我们还需要乘上一个 正交投影矩阵 :

具体的话可以再看一下这篇文章的分析 :
图形学:正交/透视投影矩阵的推导(多个思路) - 知乎 (zhihu.com)
**思考 : **
在近平面和远平面之间的点,从透视投影 -> 正交投影的过程中,它们的z轴是向近缩,还是向远拉伸???
题解:
离相机更远(更靠近远平面)