Lecture 06 : Rasterization 2 (Antialiasing and Z-Buffering)
光栅化:深度测试 和 抗锯齿(反走样)
问题描述
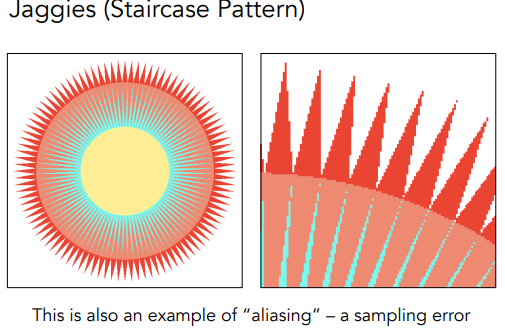
会有锯齿状…
Aliasing:走样
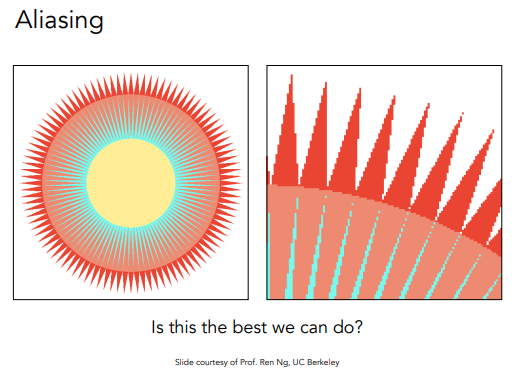
采样会有一些问题/瑕疵(Artifacts):
锯齿
摩尔纹

车轮效应

本质原因:
信号函数变换的速度太快了,导致采样的速度跟不上信号变换的速度。
解决方法
方法:
反走样(抗锯齿):
- 先对信号进行模糊;
- 再采样;
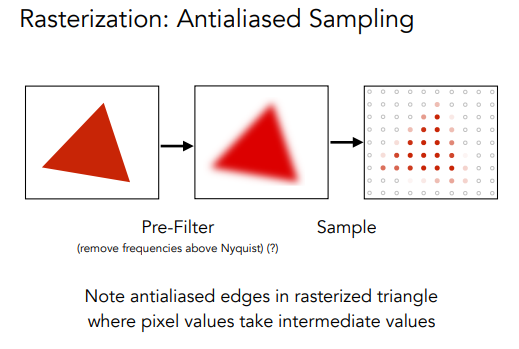
注意:这两个步骤的顺序不能反着来!!!
思考问题:
那么问题来了:
为什么这么做可以反走样呢?
为什么不能反着来呢?
具体分析:
首先总结一下走样原因:
采样的频率跟不上信号变化的频率;
从而导致,同样一个采样频率,采样两个信号函数,会导致相同的采样结果;
从而出现 “走样”。
走样原因分析:
首先解释为什么信号变换很快的时候,采样速度跟不上会导致走样的情况?
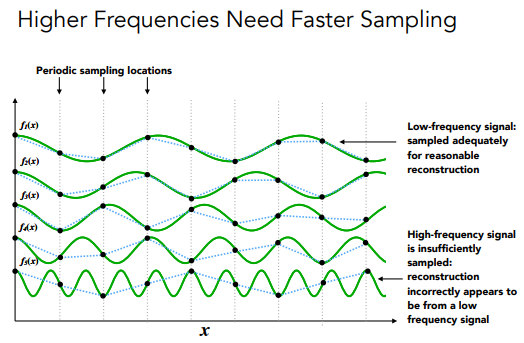
看上面这幅图,当信号变换越来越快的时候,说明信号函数的频率很快也就是比较密,图中虚线表示采样时刻,那么我们可以发现,当变换越来越快的时候,采样出来的点组成的函数越无法表现真实的函数!
接着我们看下面这张图:
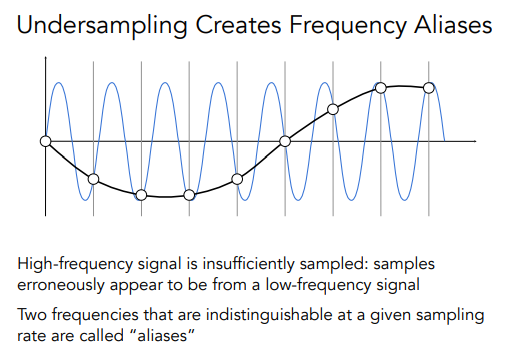
可以发现,对于相同的采样方式,对蓝色的函数和黑色的函数进行采样,得到的是相同的结果!
因此这就是走样!
傅里叶变换的作用:
滤波:过滤掉一些特定的频率

傅里叶变换可以把一个函数从时域变成频域!
也就是说:傅里叶变换能够让我们看到任何信号在各个频率下长什么样。(频谱)

上面这张图是原始图像
(左边是时域下的,右边是频域下的,表示的是同一张图哦!)
在频域的表示形式下,我们用亮度来表示信息的图像多少(在这个频率亮度越亮,表示这个频率的信息越多)
其实我们可以发现,很多图像的信息都集中在低频处。
接着,我们看下面这几个例子:
- 当图像通过高通滤波后变成下面这样:
边界的地方是高频的(因为突然发生了变化),通过高通滤波(只让高频的通过),就保留了边界

- 低通滤波
模糊了边界

- 某一段特定频率
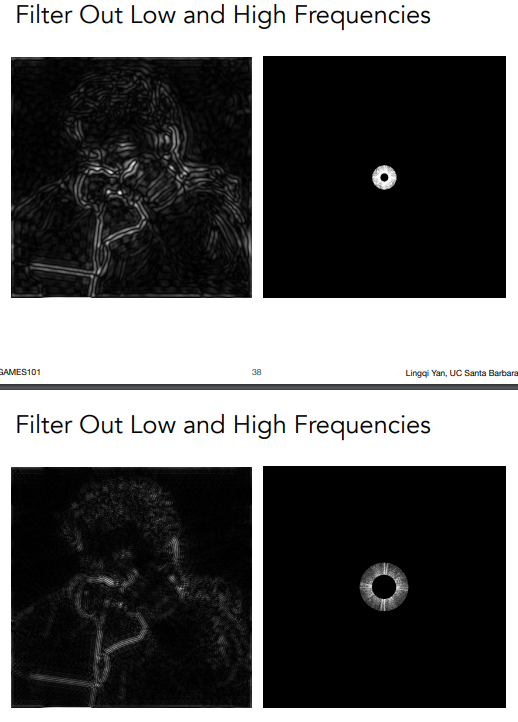
滤波
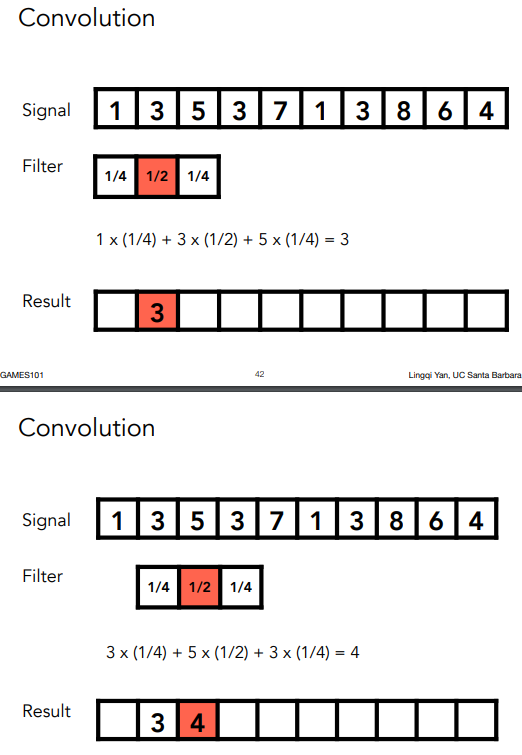
滤波 = 卷积(= 平均)
首先理解一下卷积
图像处理中的卷积我们可以简单理解为下面的情况:
首先我们有一个滤波模板(滤波器),模板里面有对应的值(概率);
然后对于每个像素值,我们都通过这个模板去计算一下,生成的值填到中心位置上。(和 数学上的卷积有所不同)
定理:
时域的卷积 = 频域的乘积
时域的乘积 = 频域的卷积
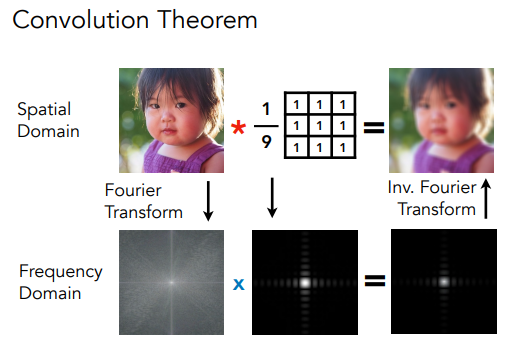
看一个例子解释:
上面这张图,通过时域范围内的卷积可以得到一张模糊的图像;等价于,我们首先将原图像和卷积模板(滤波器)通过傅里叶变换从时域转换为频域,然后将这两图像相乘,最后通过傅里叶逆变换把结果从频域转换为时域;
逻辑分析:可以看到,通过滤波器的乘积过后,原图像只保留的低频信息,也就是高频(边界)被丢弃了,导致了模糊。
同时我们也可以知道,当(滤波器)越大,一个像素将受到越多其他像素的影响,导致图像越模糊,高频信息越加被丢失!
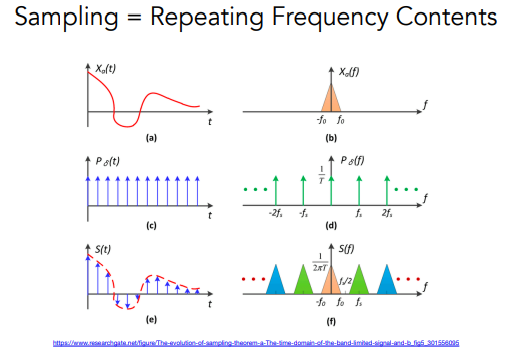
从频谱角度理解 采样:
首先,采样就是在重复原始信号的频谱;
采样越少,对于这频谱就越密,就可能发生混叠现象,也就是走样。
反走样
怎么做?
- 先做模糊(把高频信息去除,就叫做模糊)
- 再采样
为什么?
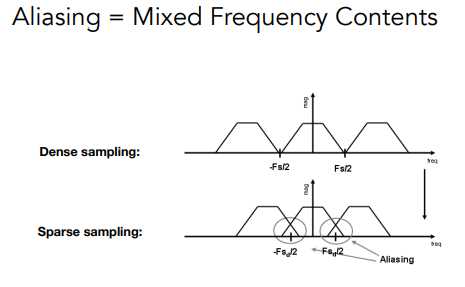
看下面这张图就知道了!
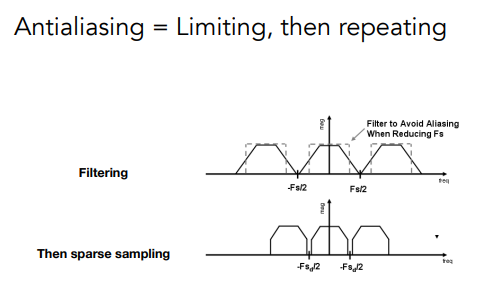
把高频的去除后发现不会混叠了!
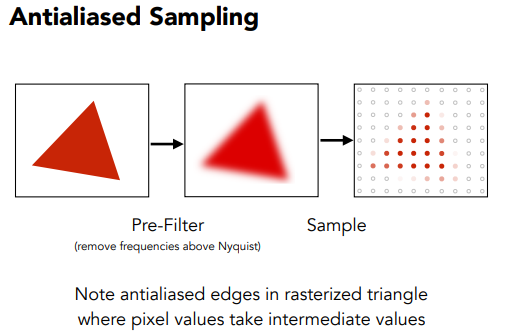
如何做?
那么怎么把图像模糊呢???
很简单啊,前面不是分析嘛,用一个 低通滤波器 和 原图像 做个卷积就行了!!!

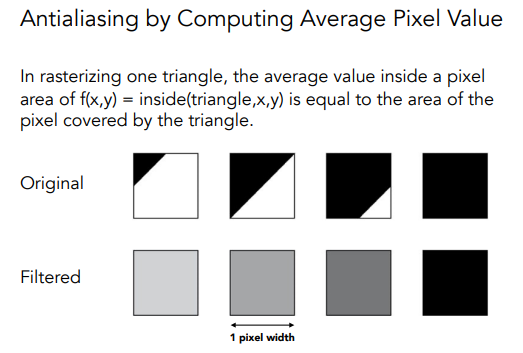
但是但是,这一步很难…
所以我们搞了一个近似的做法:MSAA
就是说,对于每个像素,我们把它分成更小的像素点,通过更多样本来近似了模糊的过程;看下面的例子(它把每个像素点分成了2x2的小像素,然后计算概率):
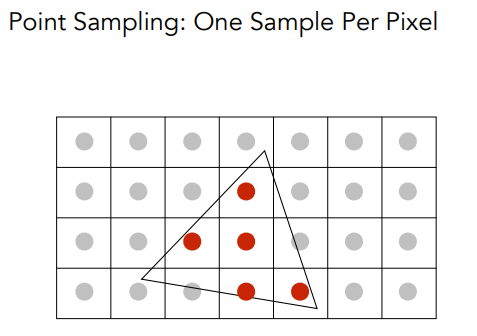
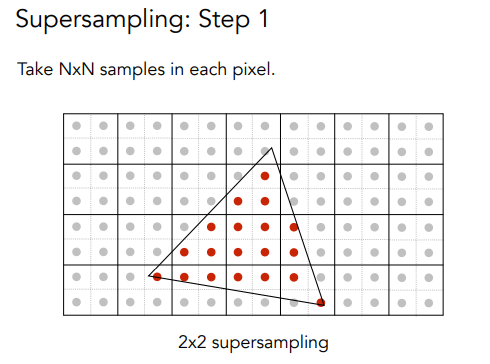
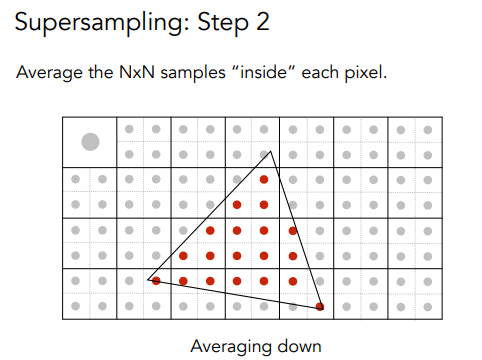
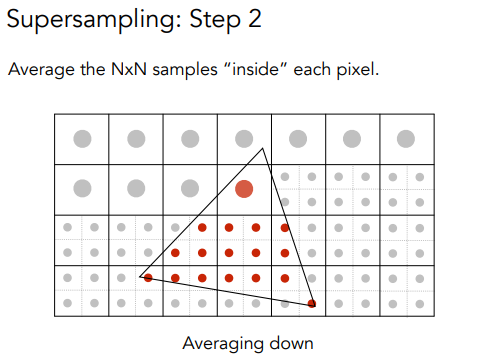
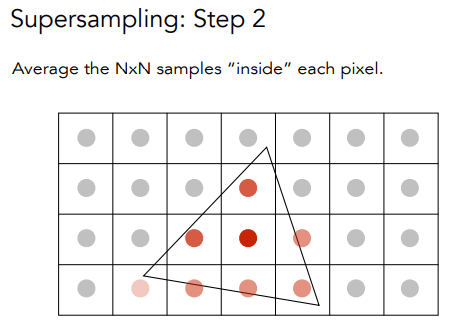
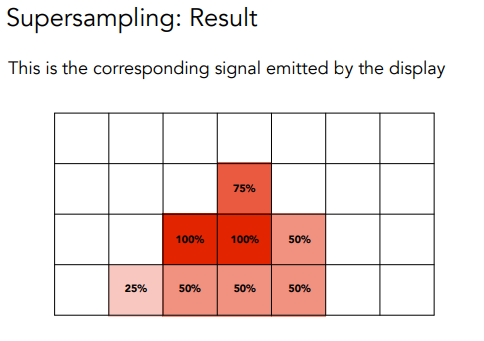
然后采样就行!
总结:MSAA 不是通过提高采样率,而是通过模糊操作来 实现反走样;
思考
缺点:
- 这么规则的分割像素,极大增加了计算量(实际生活中我们用的不是那么规则的分割,可以说是一种优化)
扩展,除了MSAA,还有其他的抗锯齿的做法: