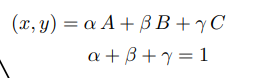Lecture 9:Shading 3 (Texture Mapping cont.)
图形学笔记(八)着色2 —— 纹理映射、重心坐标、双线性插值、Mipmap、三线性插值、各向异性过滤、纹理的应用(环境贴图、法线贴图等)
上面是笔记,记得贼全。


概述
问题:如何在三角形内部进行任何属性的插值?
什么是插值?
为什么要插值?
是因为我们想要在三角形内部得到一个平滑的过渡。
插值什么?
插值的东西是很广泛的(任意属性),比如说 颜色(三个点有三个不同的颜色,那么通过对颜色进行插值使得三角形内部的颜色有平滑的过渡);位置(我们知道了三角形的三个顶点对应纹理上的三个顶点,然后通过对顶点位置进行插值,从而确定三角形内部每个点的位置)等等。
如何插值?
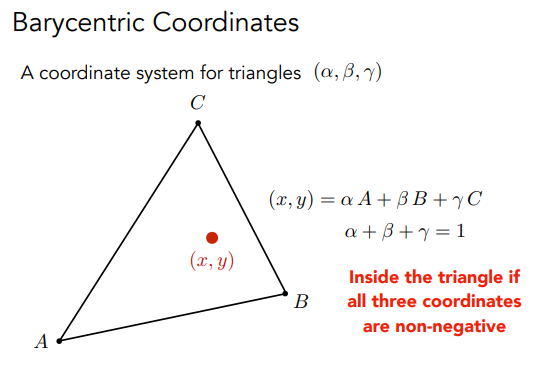
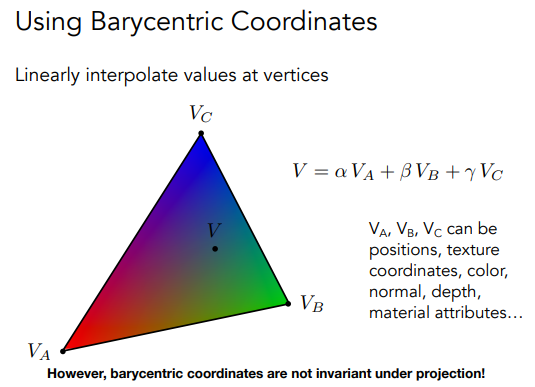
重心坐标
且三个系数非负
满足上面条件的就叫重心坐标(是三角形内的点的意思);
这里一定要注意:重心 和 重心坐标 是两个完全不同的概念!!
- 重心:指一个三角形内部的特殊点,该点与三角形的三个顶点的连线平分三角形的三条中线。
- 重心坐标:是一种表示点在三角形内部位置的方式。
- 对于一个给定的三角形ABC,点P在三角形内部的位置可以由三个重心坐标(u,v,w)表示,满足以下条件:u+v+w=1,且每个重心坐标都是点P到对应顶点的距离与三角形对边长度之比。
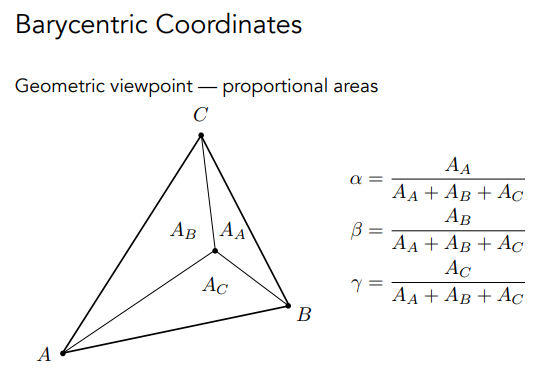
任意一点的重心坐标:
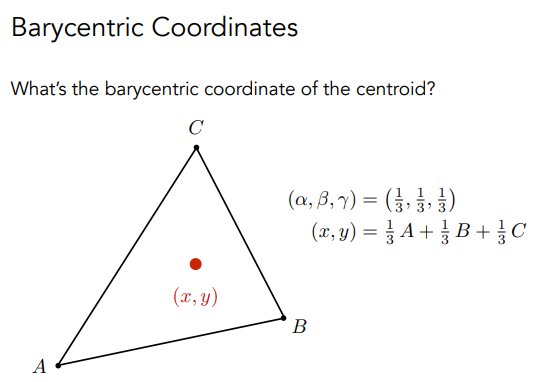
三角形的重心:
重心坐标的规范公式:
重心坐标的作用:
既然我们知道了重心坐标的计算,那么我们就能通过重心来对三角形内部一点的属性进行插值:
缺点:
当三角形被投影到其他平面上面去的时候,三角形三个顶点的位置可能发生变换,从而导致重心坐标发生变化;
也就是说,三维空间中的物体,我们不能计算投影后的重心坐标,而应该在三维空间中进行插值算出三维的重心坐标!
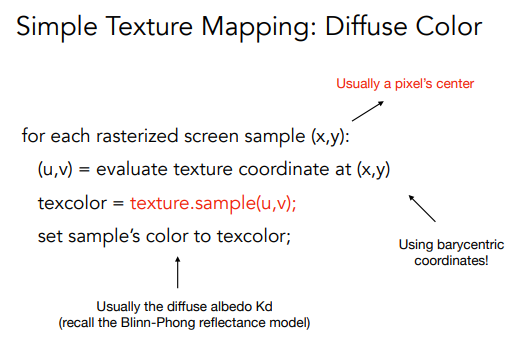
应用纹理
纹理太小的问题(双线性插值)
问题1:纹理太小的问题;
当我们的图像比较大,纹理比较小的时候,做纹理映射后纹理会被拉大,导致对应纹理位置的不是一个整数值;
导致下面Nearest的情况:
但是我们想要上面 Bilinear,Bicubic 的情况;
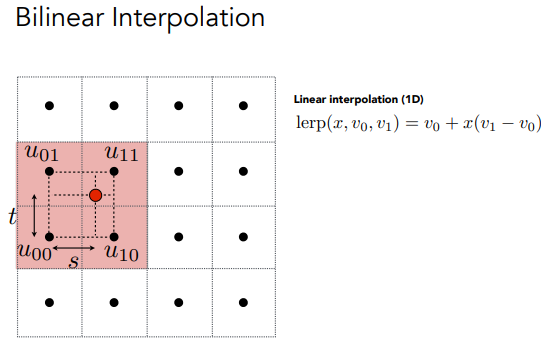
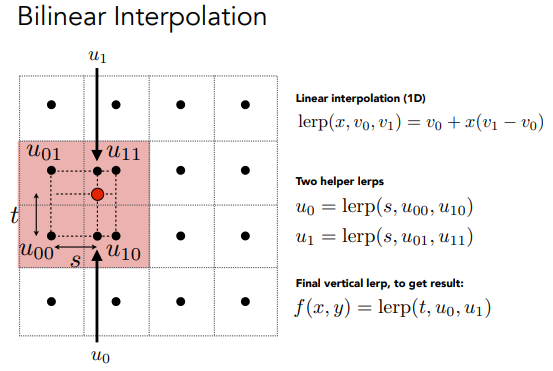
当一个像素对应的纹理坐标不是整数值时,我们如何去设置这个值???(双线性插值)
- 首选对于像素点,取周围四个点的纹理坐标
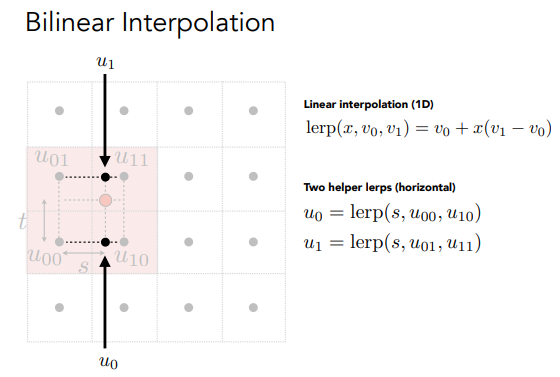
- 用U00,U10插值得到U0,用U01,U11插值得到U1。
- 用U0和U1进行插值得到红色点
纹理太大的问题(Mipmap解决范围平均值查询 + 三线性插值)
问题2:纹理太大的问题,导致走样,出现摩尔纹;
本质原因就是一个像素点包含了太多个纹理,导致当我们用普通的纹理映射的时候,这个像素点的重心代表了整个区域,从而导致了走样;
那么首先能想到的就是反走样方法:用多个像素点采样取平均值(但是计算量太大了)
换一种算法思路:不采样,直接对于每个像素点,我们可以直接知道这个像素点的平均值!
Point Query(点查询):给一个点求值(插值)
Range Query(范围查询(平均值)):给一个区域,我们能立刻得到区域中的平均值。
怎么实现范围查询???
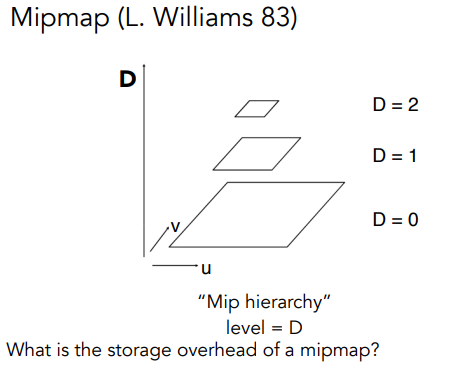
引入 Mipmap,特点:
- 快
- 近似的
- 方形查询
原理是:二进制!!!
Mipmap 具体做法步骤:
对于给定的一张图,我们先拆分成不同分辨率的图像(每次向下除二):
记住上面这个操作:
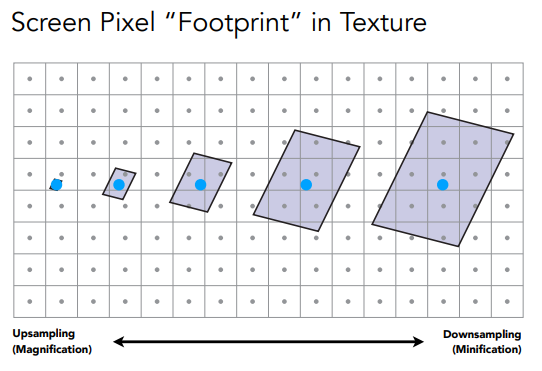
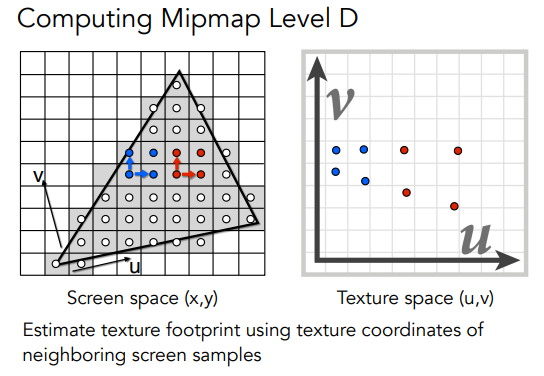
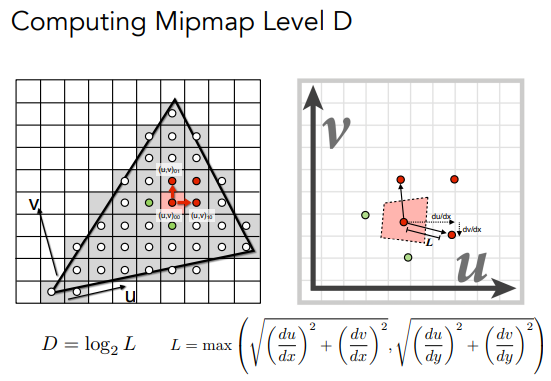
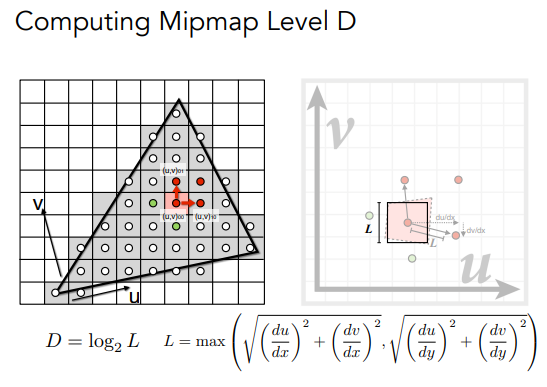
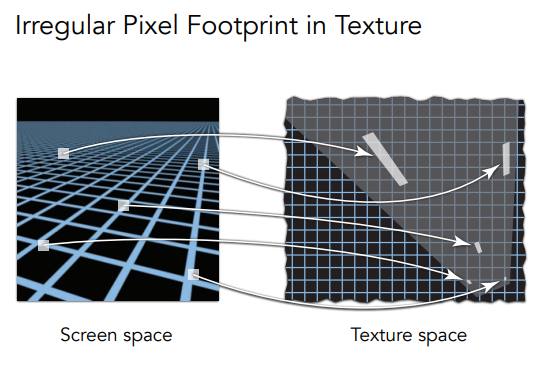
接着,对于每个像素点(在原图上面找的),我们取它周围的像素点,同时把这些点在纹理图上的纹理坐标也找出来:
接着,我们通过计算,近似的算出这个像素点在纹理坐标上大概占多少区域(不规则)
然后我们把这个不规则的区域再近似的规则成一个正方形(为什么要规则成正方形下面就知道了)
且是2的幂次
那么对于每个正方形区域,我们就能快速(O(1))的在第log2 L层去查询就行了(因为上面预处理好了!)
问题分析
但是这样会有,因为只预处理了2的幂次,我们并不知道1.5层是怎样的,所以导致不连续了;
怎么解决?
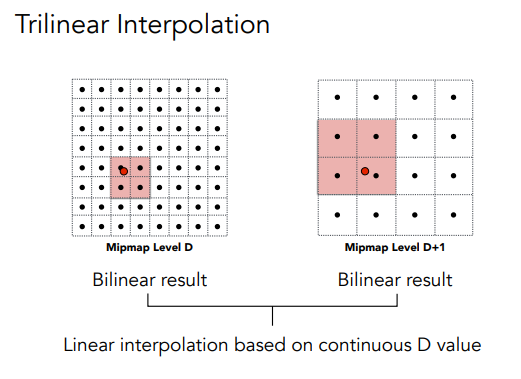
仍然是插值!
比如说,对于1.5层,我们可以选第1层和第2层,分别在层内进行 Mipmap 范围查询,然后再对这两个结果进行层与层之间的插值:(这就是三线性插值)
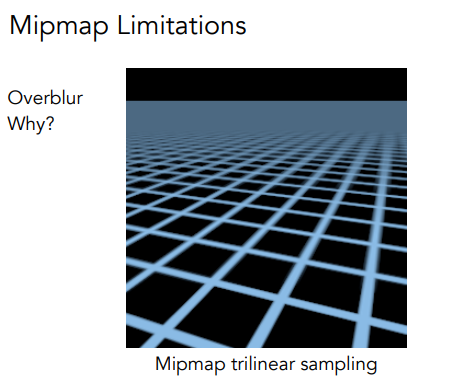
但是还是有问题:
可以发现远处细节都被模糊了…
原因是 mipmap 只考虑正方形,而有些像素对应的纹理其实可能是不规则的,从而导致模糊;
解决方法:
- 各向异性过滤
引入矩形查询的区域,但是不规则咋办…
- EWA 过滤
对于不规则形状,我们可以通过圆形的多次查询来确定;
缺点:多次查询,开销较大…
纹理的应用
靠,真的复杂…看这个笔记:
图形学笔记(八)着色2 —— 纹理映射、重心坐标、双线性插值、Mipmap、三线性插值、各向异性过滤、纹理的应用(环境贴图、法线贴图等)