Lecture 10:Geometry 1 (Introduction)
这节课主要讲:
- 纹理的应用(放在上一篇文章了)
- 几何的表示方法
几何的表示方法
- 隐式的几何表示
- 显示的几何表示
隐式的几何表示(Implicit)
概述
简单的讲就是,在空间中找到满足特定关系的点,用坐标公式表达一下;

优点:
- 很容易判断点是否在面上。(将点代入f(x,y,z),正数表示点在图形外,负数表示点在图形内,0表示点在图形上。)
- 表述起来很容易(对存储很有利)。
- 容易做面与光线求交。
- 容易描述和处理拓扑结构。
缺点:
- 不好描述复杂的形状;
- 不好知道这个面上有哪些点;
- 很难从式子中看出表示的是什么形状。
分类:
- 构造立体几何 CSG(Constructive Solid Geometry)(Implict)
- 距离函数 Distance Function(Implict)
- 水平集 Level Set Methods(Implict)
- 分形 Fractals(Implict)
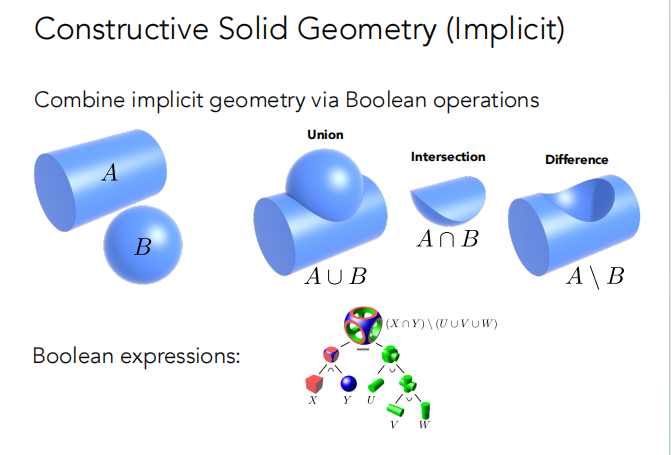
构造立体几何 CSG(Constructive Solid Geometry)
通过一系列基本几何的基本布尔运算来定义新的几何。
距离函数 Distance Function
给出任何一个位置到物体的最短距离。对一个点不描述表面,而是描述点到表面的最近距离。
把两个物体的距离函数都算出来然后把两个距离函数做融合(blending)
这个挺妙的;

比如:混合一个移动的边界
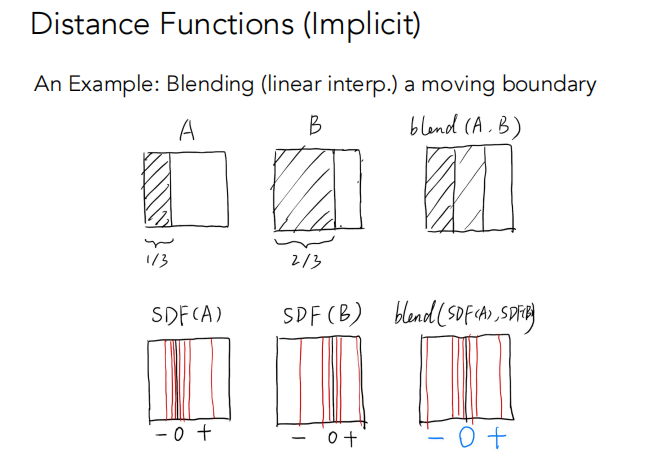
通过blend两个SDF可以得到移动后的边界。
分别求出两个物体对应的距离函数, 然后把他们blend起来,然后恢复成原本的面(找出SDF 的值为0的位置)
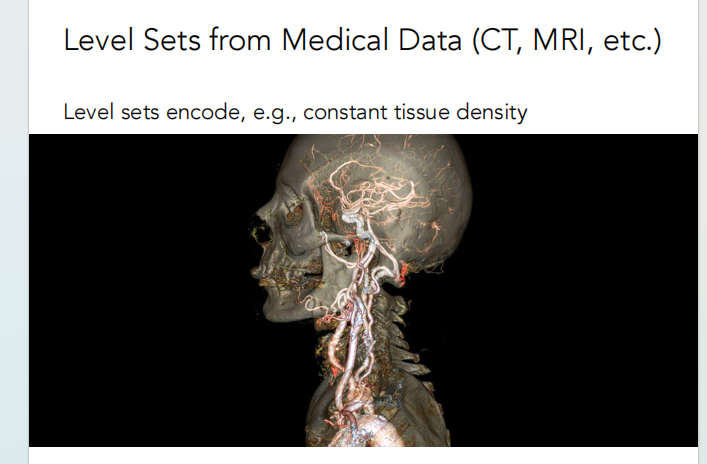
水平集 Level Set Methods
封闭形式的方程很难描述复杂的形状,所以选择一种替代方案:
存储一个值近似函数的网格(可以是二维的也可以是三维的)
通过找到插值为0的位置来找到表面,它具有一个对形状更加显示的控制。

eg:如果有一个三维的纹理表示人体不同位置的骨密度,可以让密度函数=某个具体的值,然后找到所有满足这个等式的位置,就可以得到一个表面。
分形 Fractals
局部和整体相似,一直递归;
eg:雪花,西兰花等;
这些类型的几何在渲染时会造成强烈的走样。

显示的几何表示(Explicit)
概述
所有的点直接给出,或通过参数映射定义表面。
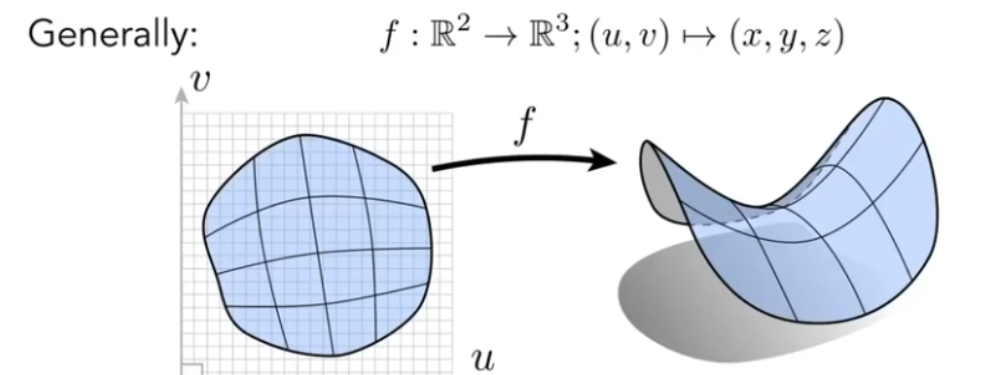
优点:对于表示形状很容易。
缺点:不好判断点是否在表面上(或内、外)。
分类:
- 点云 (Point Cloud)
- 多边形网格(Polygon Mesh)
点云(Point Cloud)
- 简单的表示为点的列表(x,y,z)
- 可以简单的表示任何一种几何图形
- 对于表示大数据集是很有用的(>>1 point/pixel)
- 经常被转换成多边形网格
- 难以在采样不足的区域画出来

多边形网格(Polygon Mesh)
- 存储点和多边形(通常是三角形或四边形)
- 容易去处理/模拟,进行自适应采样
- 数据结构比较复杂
- 图形学中最常用的表示

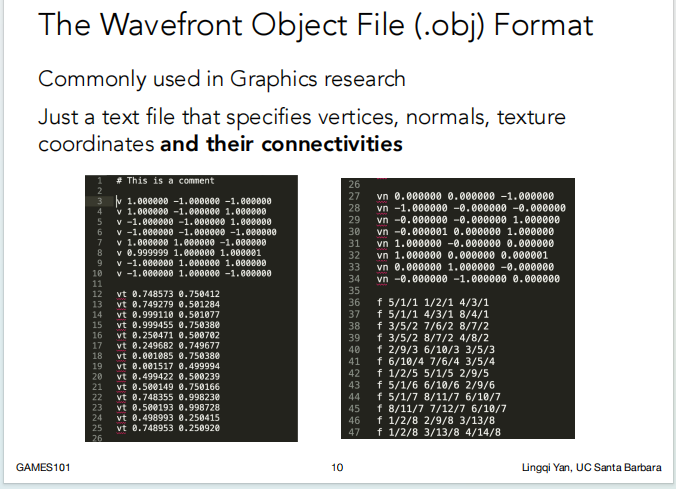
表示方式:The Wavefront Object File(.obj)格式
它是一个文本文件,由指定的顶点、法线、纹理坐标和它们的连接组成。
如下图表示了一个立方体:
v是顶点坐标
vn是法线(多了两条是因为建模误差)
vt是纹理坐标
f(face)表示面,比如f 5/1/1 1/2/1 4/3/1 表示这个三角形面是由第5、1、4个顶点组成的,三个点的纹理坐标是第1、2、3对应的纹理坐标,这个面的法线是第一条法线。