Lecture 11:Geometry 2 (Curves and Surfaces)
概述
这节课主要讲了几何中的 曲线 和 曲面;
前面一段是在讲几何的显示表示,放在放一篇文章了;
贝塞尔曲线
概述
用一系列的控制点来定义某一条曲线。这些控制点使用切线来定义贝塞尔曲线。
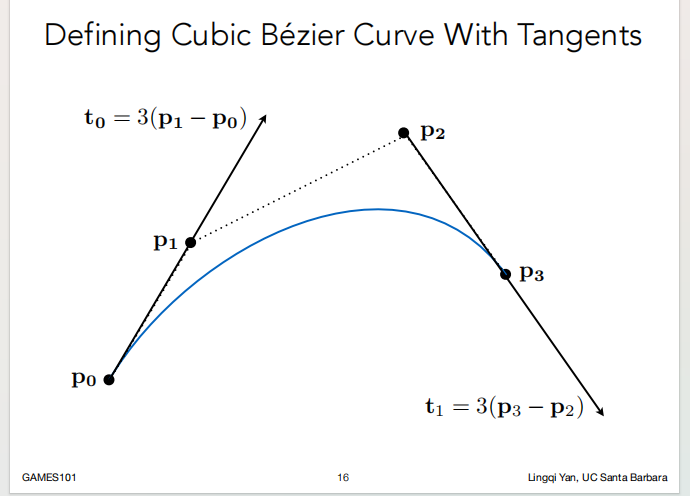
看上图,注意曲线起始方向沿着P0 P1,结束方向沿着P2 P3;
(不要求曲线经过控制点,但一定要经过起止点 和 极值点(控制点关于时间插值出来的点))
计算贝塞尔曲线——de Casteljau 算法
首先我们把整个曲线映射到 [0,1] 的时间轴上;
曲线上的每个点都是关于时间 t(0,1 之间)的插值的结果;
这也是为什么贝塞尔曲线是显示的表示(做了映射);
下面看看是如何具体做映射的:
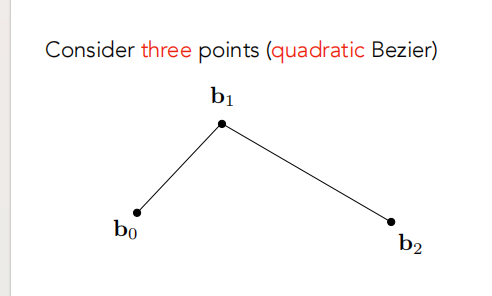
- 给定三个控制点生成的贝塞尔曲线称为二次贝塞尔曲线(quadratic Bezier)。
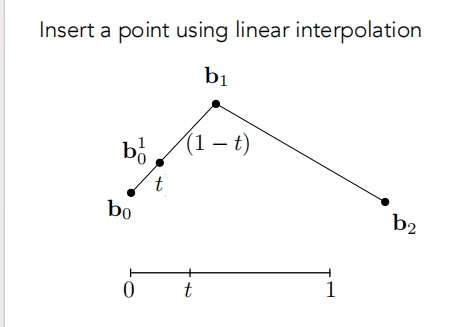
- 使用线性插值插入一个点(假设起点是时间0,终点是时间1),假设当前这个点对应时间轴的上 t ,按时间轴的比例,标记出一个线段上的插值点 b01;
- 对于每个第一层(原始的)线段都做一下插值,变成:
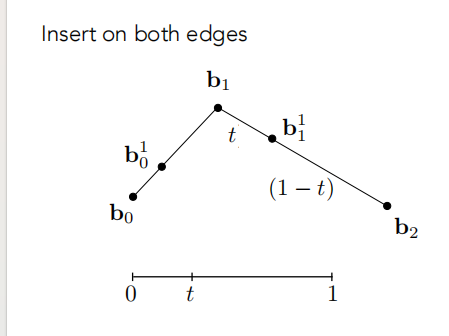
- 然后继续,同理,对于第二层的线段也同样操作,直至剩下一个点;
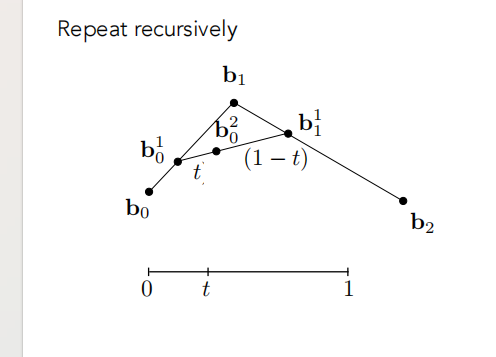
- 这样我们只是得到了一个 t 的插值后的点,我们对 [0, 1] 所有的 t 都进行插值,最终就能得到这个曲线;

贝塞尔曲线代数公式
推导:

如果有n+1个控制点(从0开始编号),可以得到n阶的贝塞尔曲线。

Bernstein 多项式:
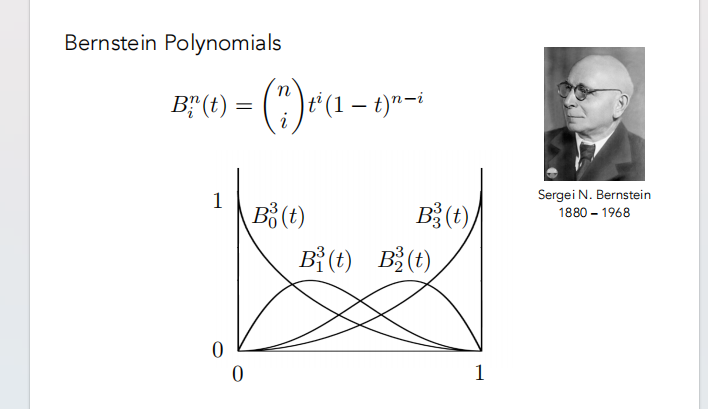
例如,当 n=3 时,公式为:
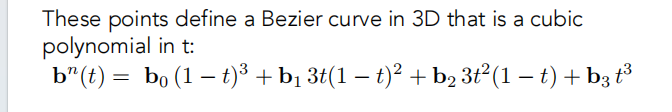
贝塞尔曲线的性质

逐段(Piecewise)贝塞尔曲线
概述
由于当控制点太多,曲线难以被控制点控制。
所以逐段定义贝塞尔曲线(一般用四个控制点)。
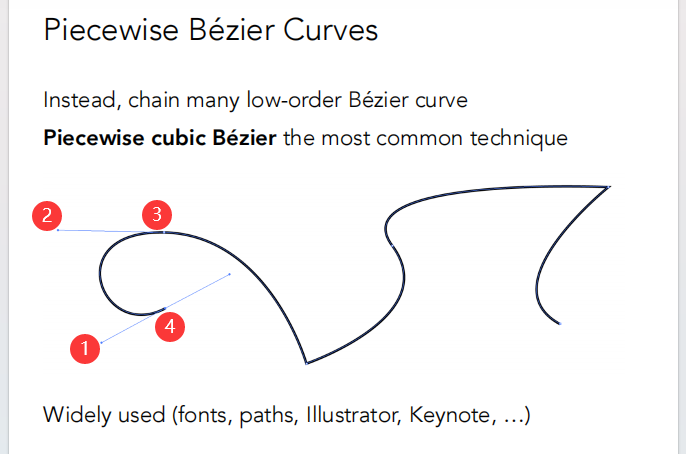
如果要让不同的分段之间光滑过渡,只需要在切线上连续(方向和大小上)。
分段贝塞尔曲线的连续性

其他类型的曲线
样条 Spline
一个连续的曲线是由一系列控制点控制点,在任意一个地方可以满足一定的连续性。
简单来说就是一个可控的曲线。
B样条 B-Splines
- 贝塞尔曲线的扩展(具有局部性,容易控制),就是基函数(basis)样条。
- 比贝塞尔曲线需要更多的信息。
- 满足贝塞尔曲线的所有性质。
- 难
(贝塞尔)曲面
概述
把贝塞尔曲线的概念延申到平面上。

回顾一下,每段贝塞尔曲线是4个点的线性插值的结果;
所以,每一片贝塞尔曲面是16控制点,两次线性插值的结果:
第一次先 4 组(每组四个)进行一次线性插值,得到四条贝塞尔曲线,然后对于四条曲线,我们再插值一次,得到曲面:
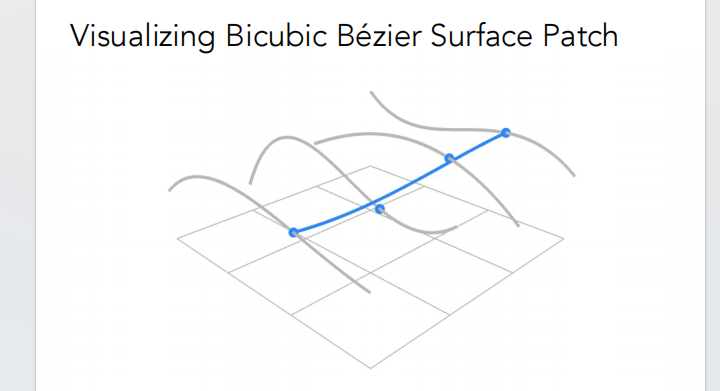
规范的讲:
输入:4*4 控制点
输出:一个在 [0,1] ^2 内的 (u,v) 参数化的二维曲面
反过来讲,给一个 贝塞尔曲面上参数化后的 (u,v),我们就能知道 (u,v) 对应的是曲面上的哪个点。