Lecture 12:Geometry 3
概述
这节课主要讲的是 曲面细分,曲面简化 和 阴影;
这篇文章记录 曲面细分 和 曲面简化,阴影放在下一篇文章;
曲面细分
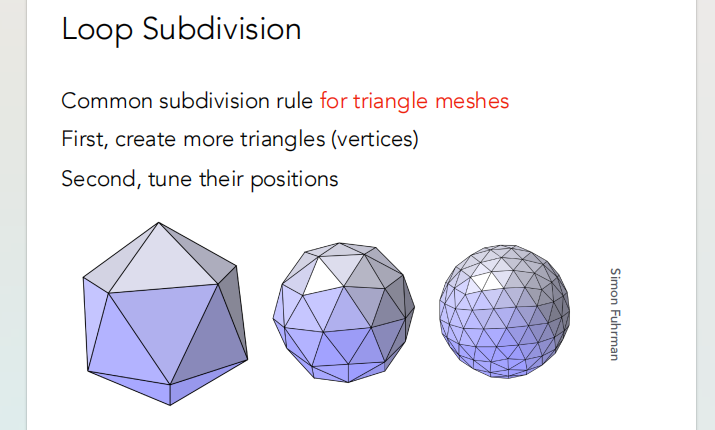
曲面细分一般来说,需要先增加点的数量,然后再调整点的位置。
Loop细分
概述
整体步骤:
- 增加三角形数量;
- 改变三角形位置,让模型看上去更加光滑;
具体算法
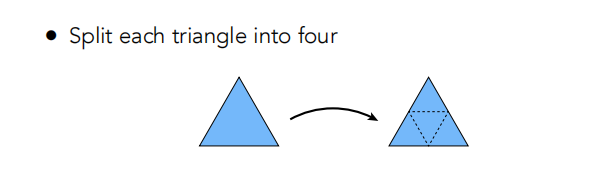
- 把每个三角形分成4个(这里就会产生新的顶点)
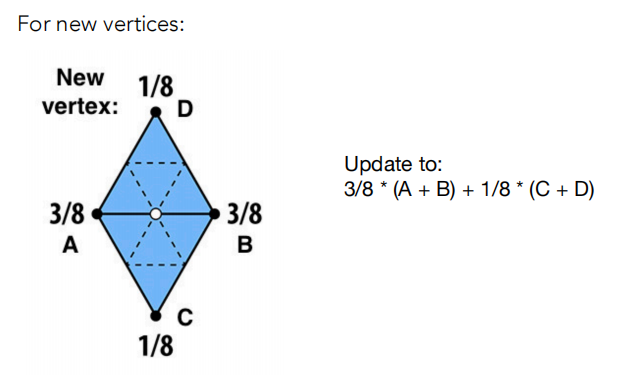
- 根据权重分配新的顶点(新顶点和旧顶点的调整方式不同)。
- 更新 新顶点:周围几个点的加权平均;
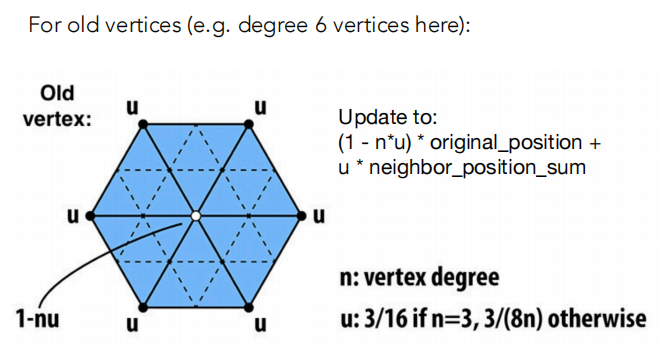
- 更新 旧顶点:根据自己原本的位置和自己周围顶点的位置来进行加权平均(n是顶点的度数)
Loop细分结果
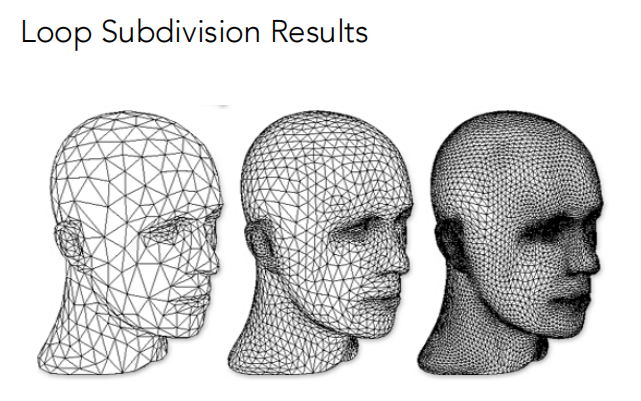
Catmull-Clark细分(General Mesh)
Loop 细分只能解决三角形网格的细分问题,对于一般的情况(一般的网格面)可以采用Catmull-Clark细分。
基本概念
非四边形面(Non-quad face):顾名思义。
奇异点(Extraordinary vertex):度数不为 4 的点。
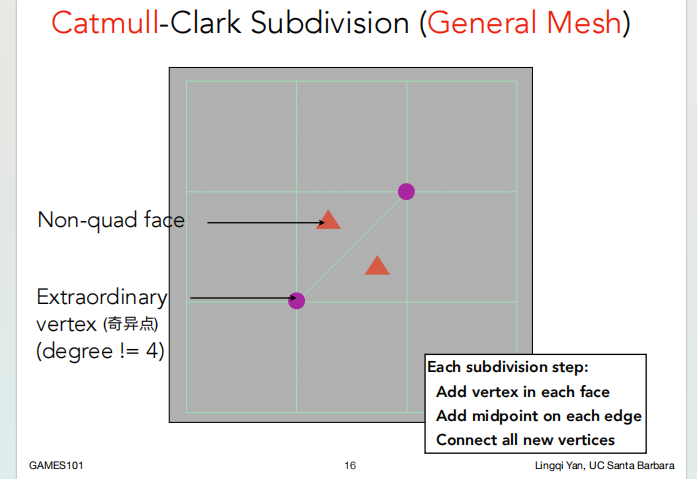
Catmull-Clark细分算法
- 增加新的点
- 取每个面的一个点(比如重心)
- 取每个边的中点
- 将所有新添加的点做连接
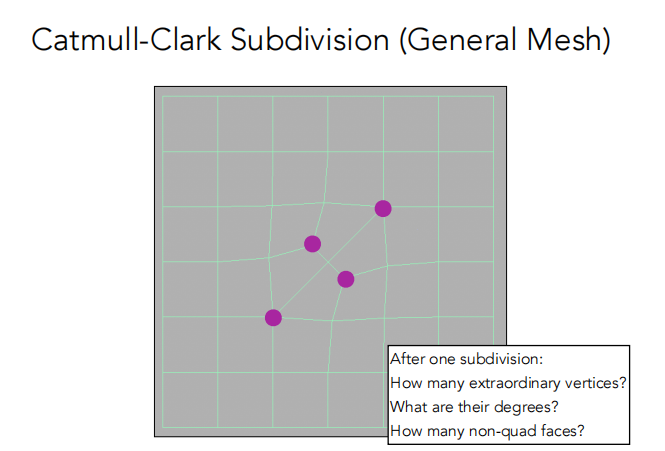
- 在一次细分后会引入两个新的奇异点。
- 新奇异点的度数为3,其他奇异点的度数不变。
- 经过一次细分,所有非四边形面会消失。
- 细分之后,每个非四边形面都会变成一个奇异点(以后再细分奇异点和非四边形面都不会发生变化了)。
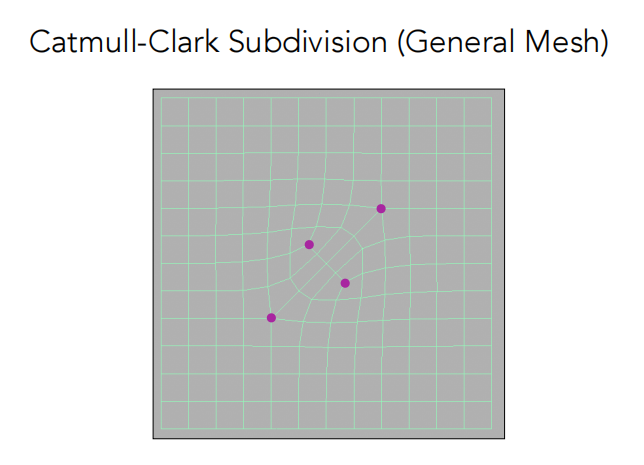
- 调整规则
- 对于 新点,面上的点和边上的点位置更新规则如下:
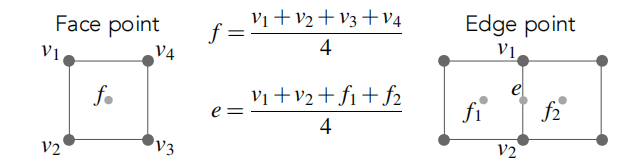
- 对于 旧点:
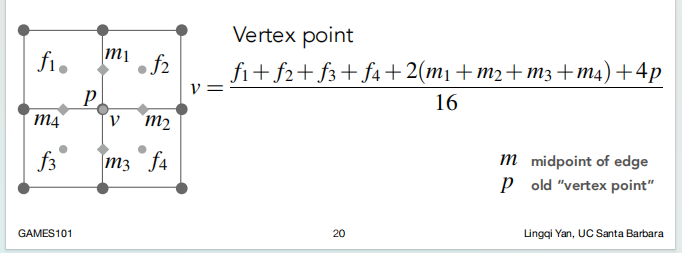
Catmull-Clark细分结果
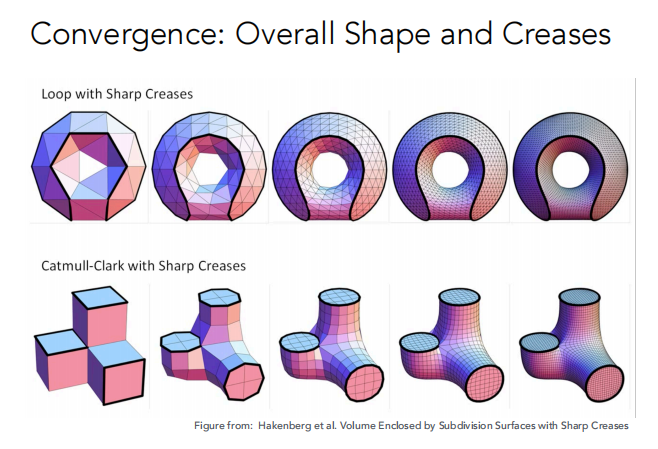
曲面简化
概述
目标:减少三角形的数量并保留整体的形状。
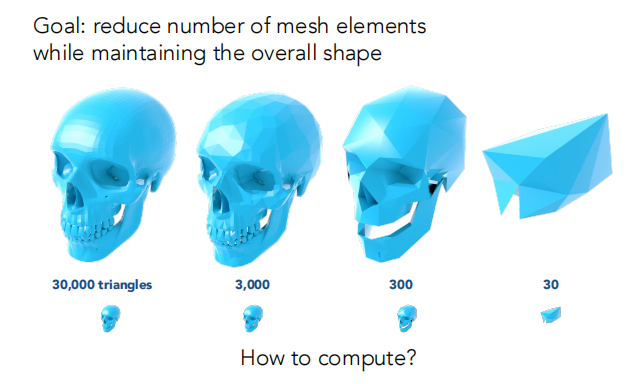
做法:边坍缩(Collapsing An Edge)
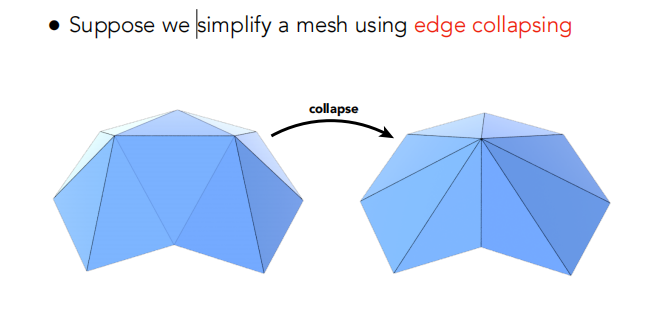
优化:二次误差度量
二次误差度量(Quadric Error Metrics)
- 它用来表示曲面简化带来的误差的大小。
- 用局部顶点做平均效果是不好的。
- 二次误差:在平面中找一个点,使得这个点与它相关联的面的距离平方和达到最小,将这个点作为新的点;

做法:
- 首先将每条边的二次误差值,作为他们各自的分数;
- 首先选一条分数最小的,进行边塌缩;
- 此时其他边的分数会变化,所以更新所有边的分数;
- 然后继续重复上面的操作;
(可以用堆来实现,是贪心算法的结果)
