Lecture 13:Ray Tracing 1 (Shadow Mapping,Whitted-Style Ray Tracing)
概述
这一节课主要讲了 阴影 和 光线追踪;
光纤追踪这一部分有点难啊…
挺抽象的,不太好理解…
Shadow Mapping
概述
Shadow Mapping本质是一种图像空间的算法。
我们之前学的都没有考虑到阴影,现在考虑一下这个东西;
具体算法
- 从光源渲染,从光源看场景,可以求出深度图(点到光源的深度)(z-buffer)
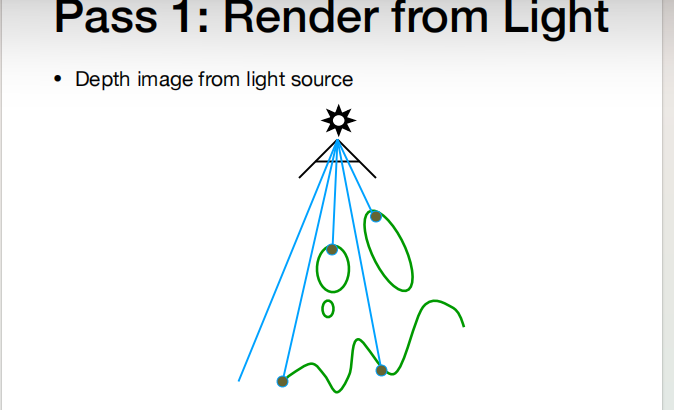
- 从相机渲染,也就是从相机发出光线,可以得到我们看到的点,然后求这些点到光源的深度;如果这个深度和从光源渲染的深度是一样的,则说明这个点没有被遮挡;否则说明,这个点被遮挡了;

结果

问题分析
- 生成的是硬阴影(只对点光源(没有体积))。
- 阴影的效果取决于shadow map的分辨率。
- 涉及浮点精度比较的问题,导致渲染出来的效果一般。
软阴影和硬阴影
下面图中,左上是硬阴影,左下是软阴影;

软阴影的原理
由于点光源有大小,会形成本影(Umbra)区域和半影(Penumbra)区域。所以会形成阴影的过渡。
进行光线追踪(Ray Tracing)的原因

- 难以做软阴影;
- 难以表现光线多次弹射,比如间接光照;
- 光栅化很快但是质量较低;
- 光线追踪很准确,但是很慢;
光栅化:实时(游戏),光线追踪:离线(动画)。
光线追踪一帧就要花10K个计算机小时
光栅化和光线追踪都是成像方式。
光线追踪(算法)
光线的一些定义概念
光线沿直线传播。
光线和光线不会发生碰撞。
光线会从光源发出,打到场景中,经过反射折射等最终进入人眼(光线具有可逆性)。
光线投影(Ray Casting)
光线投射是光线追踪中用于生成初始光线的第一步。
通过每个像素投射一条光线来生成图像
通过向光源发送光线来检查阴影
具体的讲:
- 从视点开始经过像素获得与场景中物体最近的交点。
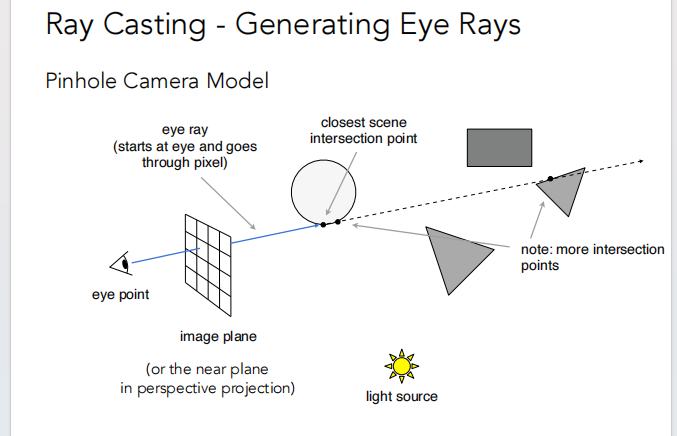
- 将交点和和光源连线,判断这个点是否对光源可见,从而确定该点是否是阴影;
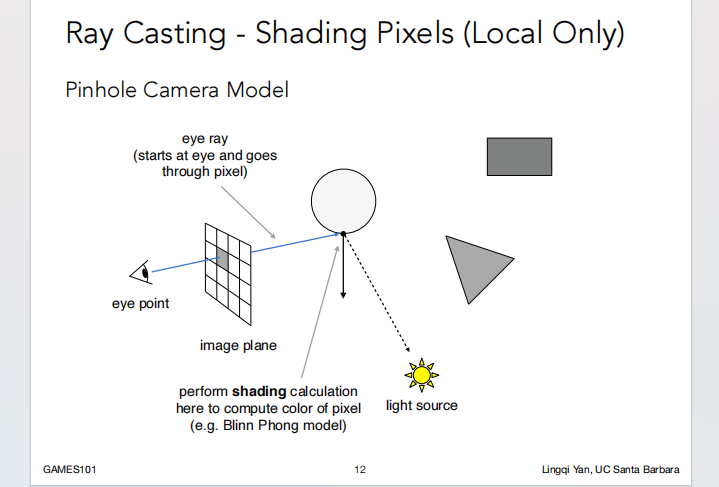
- 然后计算着色,并将结果写回像素;
Recursive(Whitted- Style) Ray Tracing
这个光线追踪算法可以看成是优化,它考虑了反射和折射的光线。
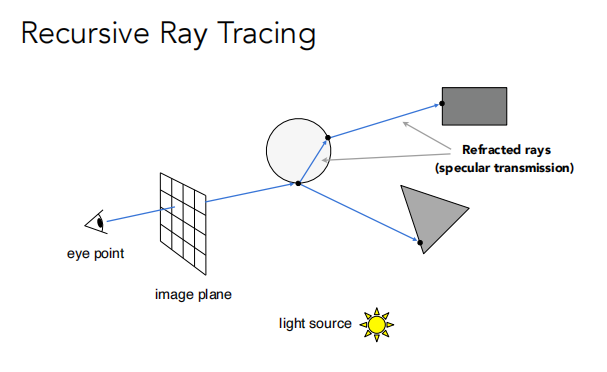
对每一个弹射点都要计算着色的值,然后把所有着色的值都加到像素的值里面去。
当然这里需要考虑能量的衰减:
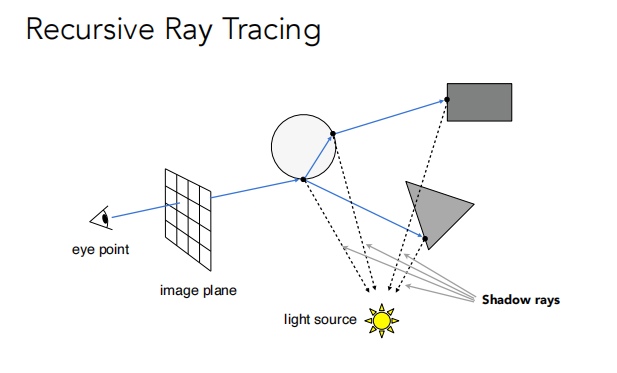
光线有不同的分类:
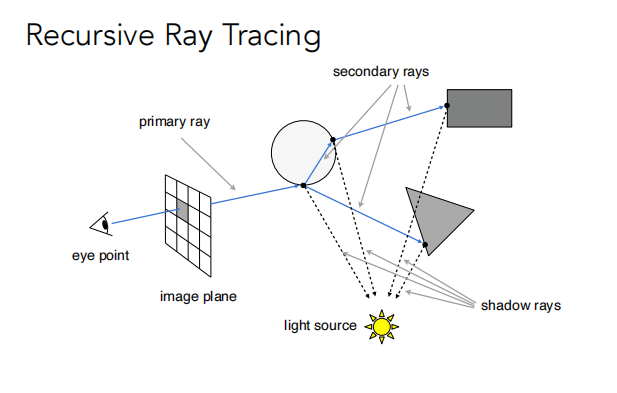
上面只是讲了大概应该怎么做,下面具体的讲细节。
光线和表面的交点(Ray-Surface Intersection)
回顾一下上面,首先光线追踪的第一步,是不是要求一条光线和表面的交点?
基本概念
光线
光线在数学上定义成 有起点和方向的射线,用 t 来表示时间,则我们可以得到射线的一个表达式:

- r(t):是 t 时刻射线上的点;
- o:是起始点;
- d:表示方向,感觉可以理解为速度;
平面
通过一个法向量和一个平面上的点来进行定义。

平面的表达式 平面是满足下面条件所有p点的集合。
光线 和 球 求交
这个很简单,带进去就行;
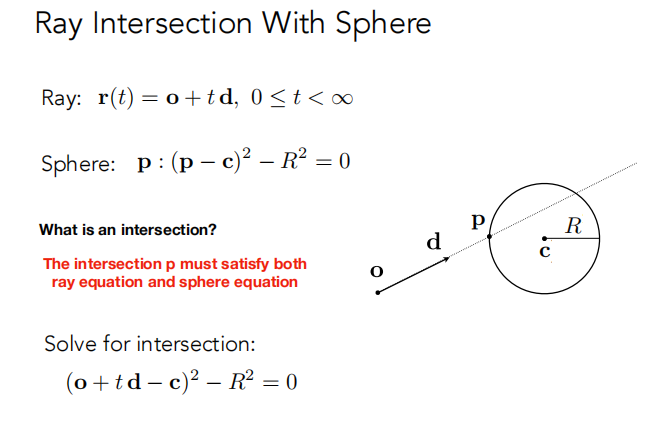
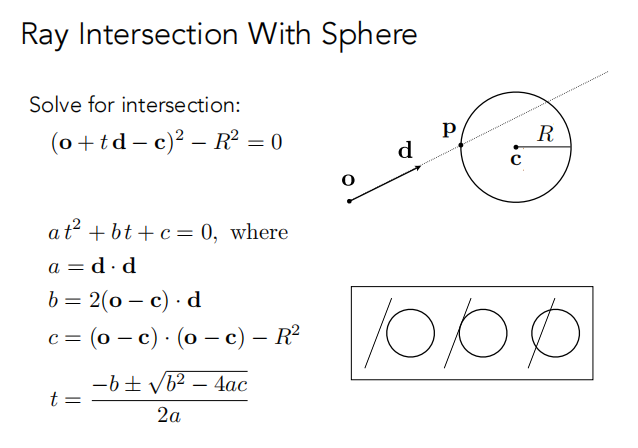
光线 和 隐式表面 求交
也是一样的,带入:

光线 和 三角形面 求交
为什么
光线和三角形求交有如下作用:
- 渲染:可见性、阴影、光照…
- 几何:可以判断点是再物体内还是物体外。
对任何一个封闭的曲面,在内部找一个点,如果点在形状内,那么从这个点发出的任意方向的射线与此物体的交点数量一定是奇数。

具体算法
简单的办法是让场景中的每个三角形与光线进行求交计算,但是有如下严重问题。
- 简单但是运算量大。
- 可以有0或1个交点。
因为三角形在平面内,所以可以把光线和三角形求交拆成两个问题:
让光线与平面求交(目前与平面求交比与三角形求交容易)。
判断与平面的交点是否在三角形内。
也就是说:光线与平面求交再判断是否在三角形内!
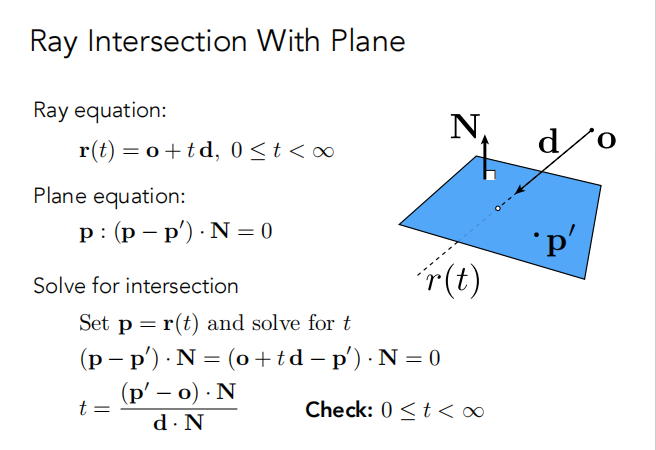
通过上面的图,可以求出 t,进而求出 r(t) (也就是交点);
然后再判断交点是否在三角形里面;
Moller Trumbore (MT)算法
通过上面我们可以知道,我们需要两步来求解;
MT 算法通过使用重心坐标来同时判断点是否在三角形里面;
在下面的式子中,左边是光线的表达式,右边是三角形上一点的重心坐标形式。
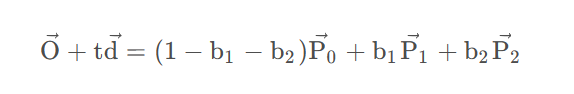
根据上面的等式解出来 t ,b1 ,b2(三个方程,三个未知数,也可以使用克莱默法则)。
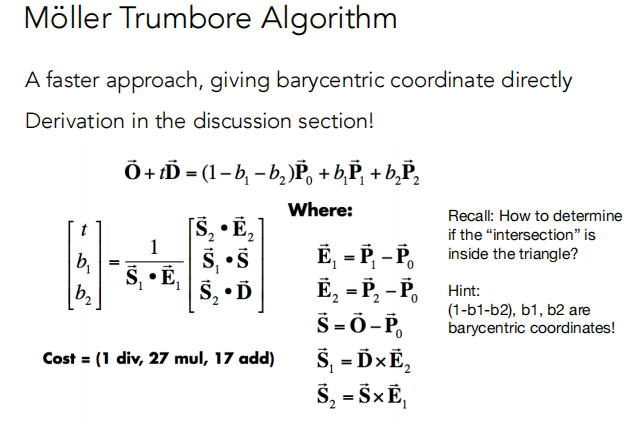
如果解出来的 t ,b1 ,b2 ,1-b1-b2 都大于0,则说明解是有意义的。
包围盒(Bounding Volumes)
概述
原始的做法是让每个像素的光线要和所有三角形面求交点,计算量太大,那么如何让这个过程加速呢?如果我们圈定包围盒,连与包围盒都不相交的三角形就不用接着算了,那么就可以很大的减少计算量。

基本思想:使用一个简单的几何体来包围一个复杂的物体,如果光线不能碰到包围盒,那么就不用再计算其与里面物体的(三角形的)交点。
这样就能少算很多很多 三角形和光线 的求交运算;
求光线与长方体的交点
3D物体通常的包围盒是长方体。
一个重要理解:长方体是三对不同的面形成的交集。
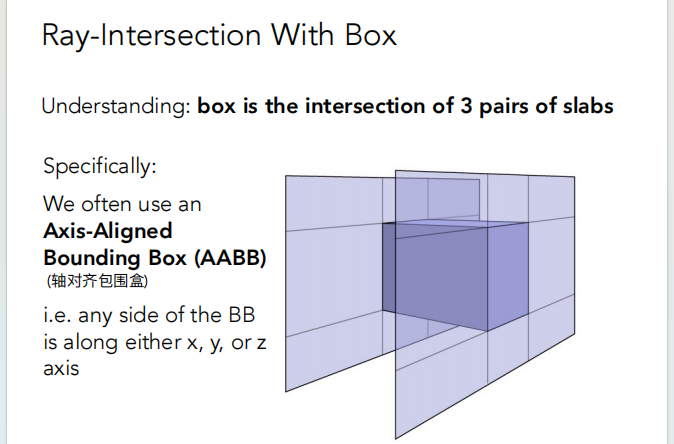
我们使用的包围盒通常是轴对齐(AABB)包围盒。Axis-Aligned Bounding Box(AABB)
经过以上分析,现在问题就变成了求光线和轴对齐包围盒的交点;
求光线和轴对齐包围盒的交点
考虑2维的情况
先分析简单的,2维的长方形;
由于前面提到的光线方程是参数方程,所以只要我们计算光线什么时候会和一对平行的边有交点(计算 t-min , t-max),就可以求出光线进入和离开这个边的时间。
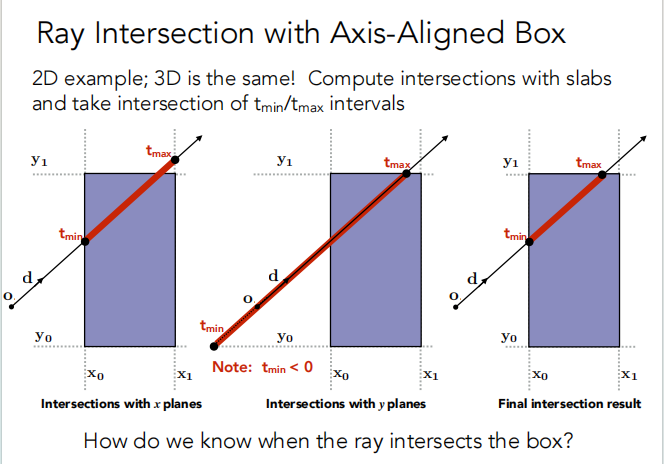
看上面的图:
首先注意到长方形有两对边;
左边的图:是求光线和左右两边的相交时的时间;
中间的图:是求光线和上下两边的相交时的时间;
然后对这两段求交集,,此时 t-min , t-max 就分别代表着光线进入和离开长方体的时间。
考虑3维的情况
根据2维的情况,我们推导出3维的情况的性质:
- 只有当光线进入了所有的对面,才能说光线进入了盒子。
- 只要光线离开任意一个对面,光线就离开了盒子。
然后通过上面我们知道,Box 有3对面,也就是每一对面,光线都能和这对面求一组 t-min , t-max;
所以再根据上面的性质可以求出光线进入 BOX 的 t (t-enter)和 离开 BOX 的 t(t-exit)
t-enter = max( t1-min , t2-min , t3-min )
t-exit = min( t1-max , t2-max , t3-max )
ti 表示第 i 对面;
t为负时的意义:
- 如果 t-exit < 0,说明盒子在光线背后,说明没有交点。
- 如果 t-exit >= 0 && t-enter < 0,说明光线的起点在盒子里,一定有交点。
结论:
如果满足 t-enter < t-exit && t-exit >= 0,则说明光线与AABB包围盒有交点。


使用轴对齐(AABB)概念的原因
主要目的是简化计算。
普通情况计算 t:
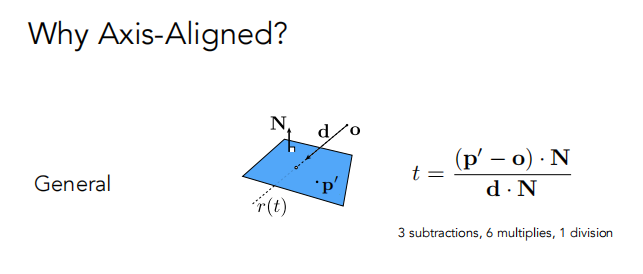
轴对齐的情况下计算t(只需要考虑各方向的分量即可):
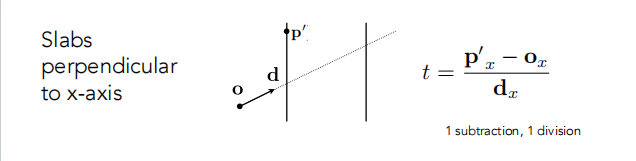
ok,这个就是这一节课的内容…
这一节课是真的多,写了好久好久…
关于包围盒只是讲了怎么做,但是还没讲怎么用(下一节?)