HomeWork 1：旋转与投影
代码：
1 | /* |
结果：
【Games 101】Lec 22：动画（续）
Lecture 22：Animation (cont.)
1 单个粒子模拟（Single Particle Simulation）
1.1 单个粒子的运动
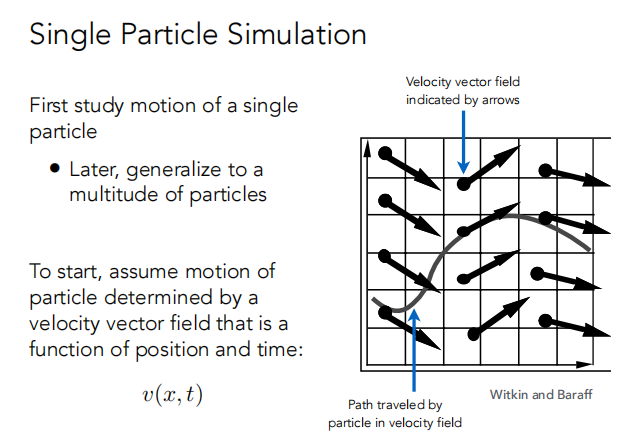
首先研究一个粒子的运动然后泛化到大多数粒子。
我们线认为粒子的运动由速度场(velocity vector field)决定，这个速度场就是一个位置和时间的函数：v（x，t）
知道粒子的位置和时间，就知道它的速度；（这个函数我们现在是已知的）
那么，计算粒子的位置（随时间变化）需要解一个一阶的常微分方程(不存在对其他变量的微分或导数First-order意味着只存在一阶导数)：
1.2 欧拉方法（Euler’s Method）
1.2.1 概述
欧拉方法是一种简单的迭代方法，经常被使用、不准确、大多数都不稳定。
可以使用欧拉方法对给定初始位置和速度场的点求解经过时间t后所处的位置。
1.2.2 误差
使用数值计算的方法积分，误差会累计，最后的Euler积分结果会很差。
1.2.3 欧拉方法的不稳定性（Instability of the Euler Method）
如下图，粒子的轨迹始终不能沿着圆形或指定的轨迹。
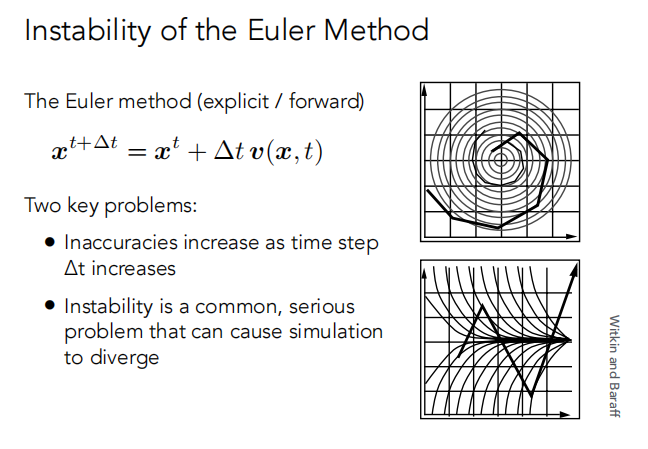
即欧拉方法有两个关键的问题：
- 误差随着时间步长 Δt 的增加而增加。
- 不稳定性是一个普遍且严重的问题，它能造成模拟 diverge。
1.2.4 Errors 和 Instability
用有限差分数值积分法求解
导致两个问题:
Errors：
- 每个时间步的误差累积。精度随着模拟的进行而降低
- 在图形应用中，准确性可能不是关键
Instability：
- 错误可以复合，导致模拟甚至发散当底层系统没有
- 缺乏稳定性是模拟中的一个基本问题不容忽视
1.3 克服不稳定性的方法
1.3.1 概述
- 中点法/修正欧拉法
- 起点和终点的平均速度
- 自适应步长
- 递归地比较一步和两个半步，直到可以接受错误
- 隐式方法
- 使用下一个时间步骤的速度(硬)
- 基于位置/ Verlet的集成
- 在时间步长后约束粒子的位置和速度
1.3.2 中点法（Midpoint Method）
- 使用欧拉方法计算，点到达A( a )。
- 使用欧拉方法计算上一步起始点与A点的导数( b )。
- 使用中点的导数来重新更新位置( c )。
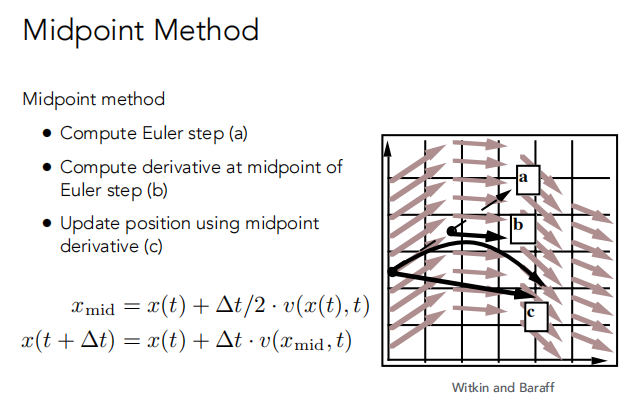
中点法比欧拉方法多了一个二次的项。
1.3.3 自适应步长法（Adaptive Step Size）
- 使用步长为T计算一个欧拉步骤来获得 X(T)
- 计算两个欧拉步骤，步长为T/2，获得 X(T/2)
- 计算error ∣∣ X(T) − X(T/2) ∣∣
- If ( error > threshold ) 减少步长并重复上面的步骤。
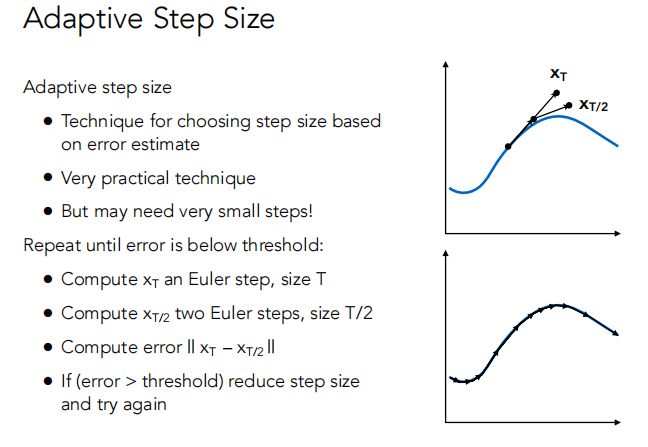
Adaptive 是基于 error 估计选择步长的方法，非常实用，但可能得到的步长会很小。
1.3.3 隐式欧拉方法
也被称作后向方法，使用下一时间的导数来计算当前的步骤。
定义与量化 “stability” （稳定性）的方法
- 使用局部截断误差（每个Δ \DeltaΔ的误差）/ 总截断累积误差（整体累加后的误差）来研究稳定性。
- 研究数的大小无意义，有意义的事研究它们的阶。
- 隐式欧拉方法的阶数为1，意味着局部截断误差为 O(h^2) 且全局阶段误差为 O(h)（h就是步长，定义为 Δt）。
- O(h)的理解:如果将 h 减半，预期误差也会减半。
1.3.4 Runge-Kutta Families
Runge-Kutta方法是一系列用于求解 ODE 的高级方法。
特点
- 擅长处理非线性问题。
- 它的四阶版是使用最广泛的，又名 RK4。
h就是步长，也就是 Δt
1.3.5 Position-Based / Verlet Integration
这是一种不基于物理的方法，通过调整物体的位置使物体满足某种性质。
思想：
- 在修改欧拉前步（forward-step）之后，约束粒子的位置以防止divergent、不稳定的现象。
- 使用约束位置计算速度。
- 这两种思想都会耗散能量，使其具有稳定性。
特点：
- 快速又简单。
- 不是基于物理模拟的，不满足能量守恒。
2 刚体模拟（Rigid Body Simulation）
刚体模拟与模拟单个粒子相似，只需额外考虑一些属性（角度，角速度）
3 流体模拟（Fluid Simulation）
3.1 基于位置的简单流体模拟方法
关键思想
- 认为水是由刚体小球组成的。
- 认为水是不可压缩的。
- 只要某处的密度海绵，就需要通过改变粒子的位置来“纠正”。
- 需要知道任何位置的密度的梯度。
- 使用梯度下降法来进行更新。
3.2 质点法和网络法（Eulerian vs. Lagrangian）
3.3 Material Point Method (MPM)
MPM 是一种混合的(Hybrid)，结合 Eulerian 和 Lagrangian 的方法。
- Lagrangian：认为粒子带有材质属性。
- Eulerian：使用网格来做数值积分。
- lnteraction：粒子将属性传递给网格，网格执行更新，然后插值回粒子。
参考
结束，下面把作业做一做，然后打算做个玩具渲染器（当作毕设了…）
【Games 101】Lec 21：动画
Lecture 21：Animation
1 概述
“Bring things to life”
- 交流的工具
- 美学引导技术
建模的扩展
- 把3d模型延申到时间的维度
输出：按顺序播放的图片序列，提供一种运动感。
- 电影：24 fps
- Video（通常）：30 fps
- Virtual reality：90 fps
2 Historical Points in Animation
这个看一下PPT就行…
3 动画技术
3.1 关键帧动画（Keyframe Animation）
- 动画师 创建关键帧
- 人或计算机 创建中间的帧
关键帧动画一般使用插值方法来进行补帧，把每一帧当作参数值的向量，下面是线性插值。
用样条进行优化：
3.2 物理仿真（Physical Simulation）
3.2.1 概述
F = ma
使用数值模拟生成物体的运动
例子：
- 布料模拟（ Cloth Simulation）
- 流体（ Fluids ）
- 质点弹簧系统（ Mass Spring System）
- 头发（ Hair ）
- 质点弹簧网格（Mass Spring Mesh）
3.2.2 质点弹簧系统（Mass Spring System）
- 简单的弹簧
理想化的弹簧：没有长度，作用力会导致位移。
胡克定律：
- 非0长度的弹簧
问题：永远震动下去。
定义概念：
引入能量损失
- 表现得像运动中的粘性阻力
- 在速度方向上减慢运动
- kd为阻尼系数
问题：所有运动都会停止（不能表现弹簧内部的损耗）。
弹簧的内部阻尼（Internal Damping for Spring）
只阻尼内部，由弹簧驱动的运动。
Viscous drag 仅限于弹簧长度的变化，不会减慢弹簧系统的整体运动(例如，整体平移或旋转)
Note: 这只是一种特殊的阻尼(damping)。
- 来自弹簧的结构
弹簧结构的连接可以决定一个图形的行为，比如改进下面的连接来模拟布料。
原来的不足之处：
- 切变会影响形状。
- 会使原来的形状不在一个平面上。
改进之后：
- 在对角线连接弹簧会抵抗切变。
- 在两个对角线都连切线避免了各向异性。
- 红色的弹簧会避免 out-of-plane bending（两条对角线竖直方向会弯折）。
其他模型：有限元方法FEM（Finite Element Method）
（代替弹簧系统的一种模拟布料的办法）
常用来做汽车碰撞，主要思想是力与力之间存在传导，效果如下。
3.2.3 粒子系统（Particle System）
- 粒子系统就是将动态的系统建模为大量粒子的集合
- 每个粒子的运动都是由一组物理(或非物理)力定义的。
- 粒子系统是在图形和游戏上很流行的技术。
- 具备可扩展性：粒子越少，速度越快，粒子越多，速度越慢。
挑战
- 可能需要许多粒子(例如流体)
- 可能需要加速结构(例如寻找最近的粒子进行如引力的相互作用)
步骤
- 创建新的粒子（如果需要的话）。
- 计算每个粒子的力。
- 更新每个粒子的位置和速度。
- 移除死掉的粒子。
- 渲染粒子。
粒子系统的作用力
- 引力和斥力（repulsion） 如：万有引力、磁力、弹力（Springs）、弹簧、推进力（propulsion）。（eg：万有引力）
- 阻力（Damping forces）：摩擦（Friction），空气阻力（air drag），粘度 （viscosity）…
- 碰撞（Collisions）：墙壁、容器、固定的物体…。与动态物体、人物身体部位等…。
模拟动物集群（Simulated Flocking as an ODE）
需要考虑一个例子的各种作用力
4 运动学 Kinematics
4.1 正向运动学（Forward Kinematics）
Articulated skeleton
- Topology 是一种拓扑结构（描述什么与什么连接）
- 关节（joints）间的几何关系。
- 树形结构
Joint types（关节类型）
- Pin（1D rotation）：在平面内旋转
- Ball（2D rotation）：可以旋转到不同的平面
- Prismatic joint（translation）：可以拉长
例子：2D中简单的两端骨骼。
Animator 提供角度，计算机决定 end-effector 的位置p。
Animation 是用角度参数与时间的函数来描述的。
优点：
- 直接控制方便
- 便于实施
缺点：
- 动画可能难以用物理的方式来制作（不直观，艺术家不喜欢）
- 消耗动画师的时间
4.2 逆向运动学（Inverse Kinematics）
概述：
根据尖端获得关节的角度位置。
Animator 提供 end-effector 的位置，计算机决定满足限制的 joint 角度。
计算方法：
问题：
- 解不唯一
- 解可能不存在
N-link lK 问题优化方法
- 选择一个初始构型。
- 定义一个 error metric（如：目标与当前位置之间距离的平方）。
- 计算误差梯度作为构形的函数
- 应用梯度下降(或牛顿法，或其他优化程序)
4.3 应用
4.3.1 Rigging 绑定
Rigging 是一套高级角色控制，允许更快速和直观地修改姿势、变形、表情等。
- 就像提线木偶的线一样。
- 捕捉所有有意义的角色变化。
- 因角色而异。
- 制作昂贵
- 具有人工误差并需要艺术和技术的训练。
4.3.2 混合形状（Blend Shapes）
直接在曲面之间进行插值。
最简单的方案：取顶点位置的线性组合，样条用于控制随着时间的推移权重的选择。
4.3.3 动作捕捉（Motion Capture）
Motion Capture 是创建动画序列的数据驱动方法。
下面是三种动捕设备（光学、磁力和机械）。
优点：
- 非常贴近真实
- 可以快速的过去大量的真实数据。
缺点：
- 准备工作复杂且高花费。
- 捕捉到的动画可能不满足艺术家的需要，需要选择。
5 动画/电影生产的 Pipeline
参考
【Games 101】Lec 20：颜色和感知
Lecture 20：Color and Perception
东西挺多的…
1 光场（Light Field / Lumigraph）
1.1 全光函数（The Plenoptic Function）
将整个世界看成是七个维度的函数：
- θ,ϕ：角度
- λ：光的波长信息（表示颜色信息）
- t：时间
- Vx，Vy，Vz：可以改变自己的位置从另外的角度看世界
P( … ) 这个函数可以表示在任何地方，任何方向，任何时间看到的东西的颜色，这个函数就是全光函数
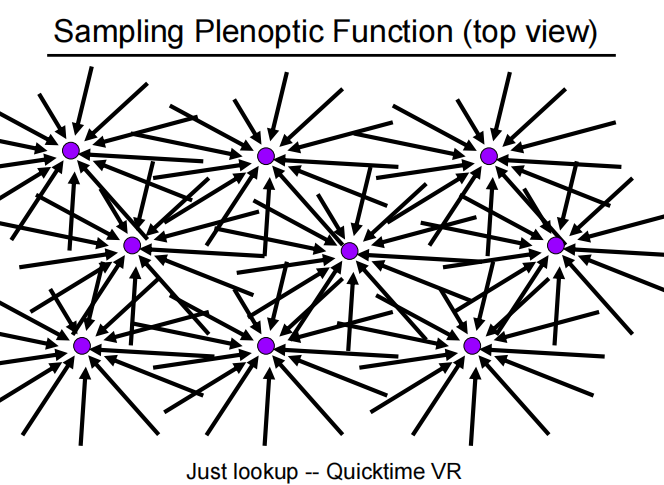
光场就是全光函数的一部分。
1.2 光线 Ray
光线是一个5D表示的，包含 3D 的 position 和 2D 的 direction。
另一种定义方式：两个点定义一条光线。
它是4D表示的，包含 2D 的 direction 和 2D 的 position。
1.3 光场
1.3.1 定义
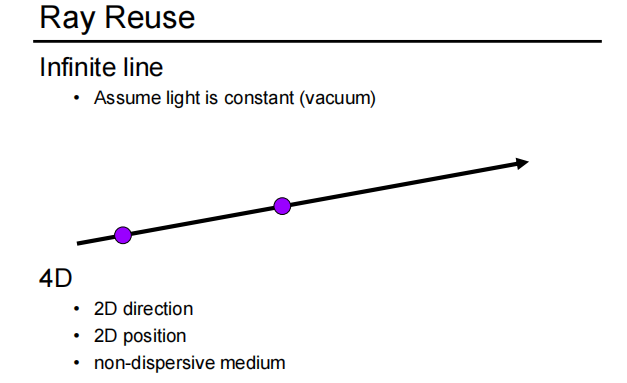
想要描述一个物体的视觉信息，只要找出它的包围盒，并记录包围盒表面任意一点向任意方向的发光情况即可。
光场就是在任何一个位置往任何一个方向去的光照强度。
1.3.2 光场的作用
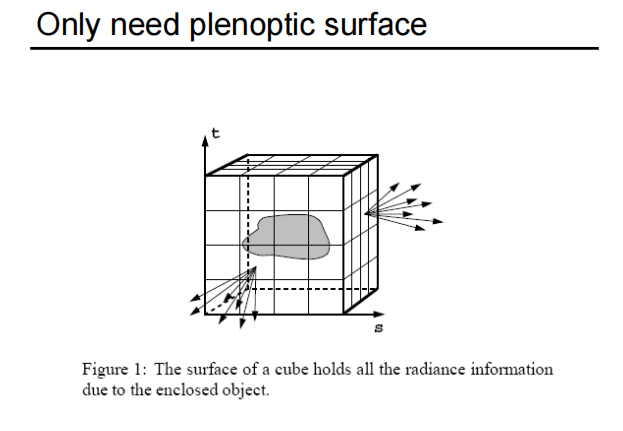
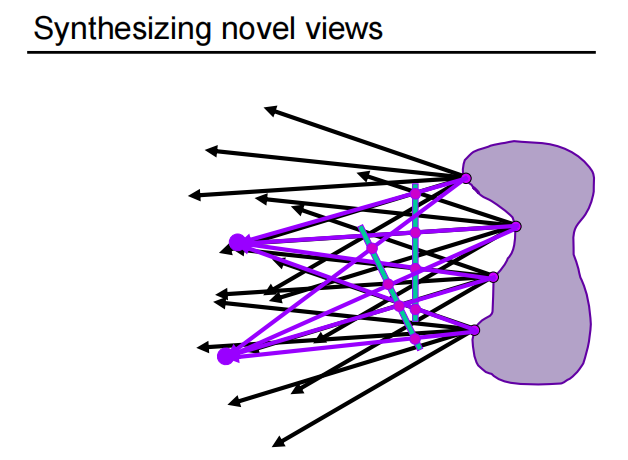
有了光场后，从任意位置都可以看向这个物体，有了视点和看向的方向，查询4D的函数就可以查询到记录的值（光的强度）。
有了包围盒之后，就可以忽略光场内部的细节，只要记录包围盒表面的任何位置任何方向的光照信息即可。
1.3.3 光场的表示方式
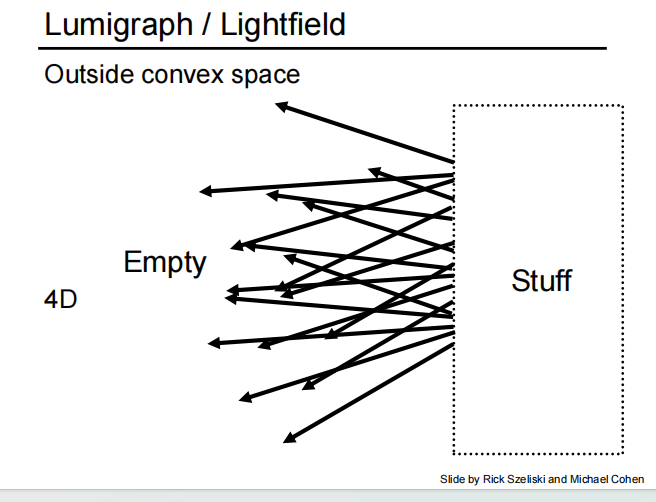
起始点 + 一个角度
两个相互平行的平面，两个点确定一条光线
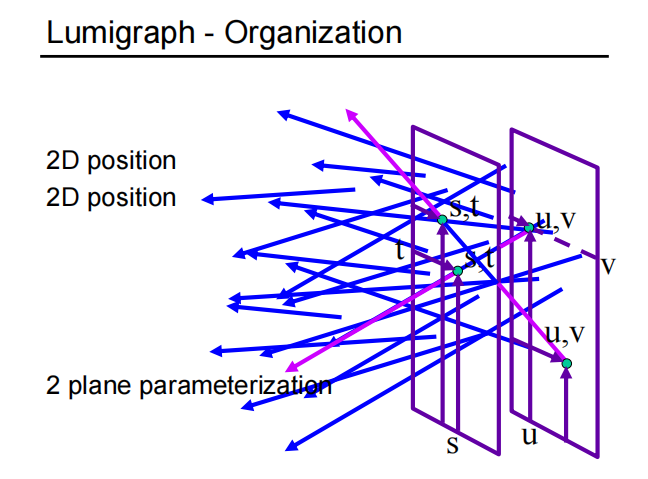
参数化的表示两个平面（s t）（u v），找到所有 uv 和 st 的对应关系，便可以定义任意一条光线。
下面看一下解释，假设整个世界在 st 面的右边：
- 固定 uv 平面点x，从这个点看向 st 面的不同的点yi，然后所有yi的集合相当于就是一张图像（改变x，相当于就是从不同的角度去看这个物体）
- 固定 st 平面上的点x，从 uv 面的不同的点 yi 看向x，那么所有的yi的集合就是这个物体的一个方向的结果（改变x，得到的就是这个物体的不同方向上的结果）
1.3.4 光场摄像机（Light Field Camera）
原理：本来是光都打在一个像素上的，但是现在把像素的位置往后移一下，原来的位置放成一个微透镜，让透镜把来自于不同方向的光分开然后记录下来，然后对于特定方向上的光线重新聚焦。
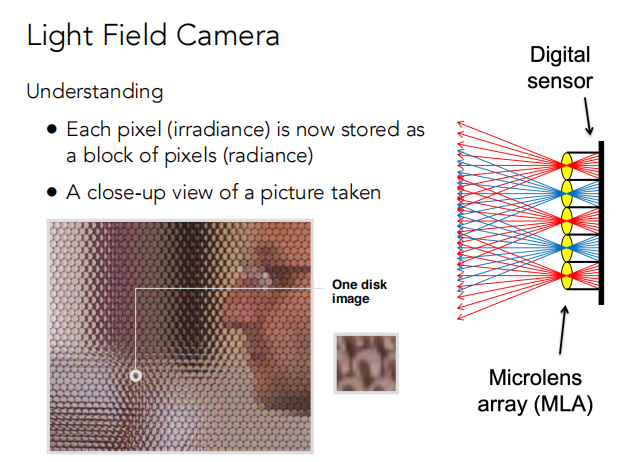
还原普通照片的方法：对于每个透镜都选择每一“块”的最底部的像素。
有了光场之后，可以虚拟移动相机的位置（重新聚焦也是一样的道理）。
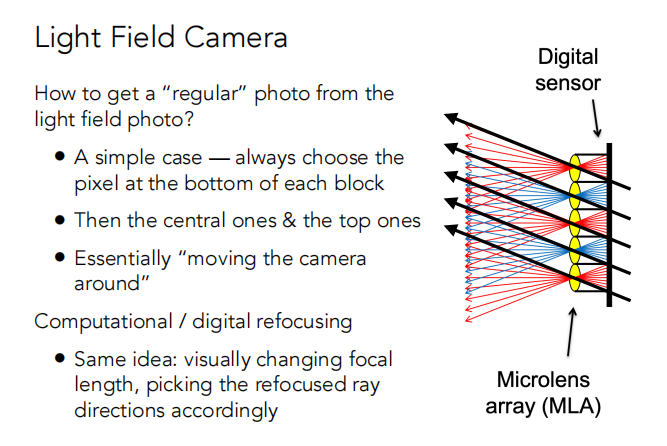
总结：光场相机能实现虚拟移动相机位置，改变聚焦等功能。
光场相机特点：光场摄像机记录了所有的光场信息。
光场相机的问题
- 光场相机的空间上的分辨率不足。
- 高成本（胶片分辨率十分高，微透镜很精密）。
2 颜色
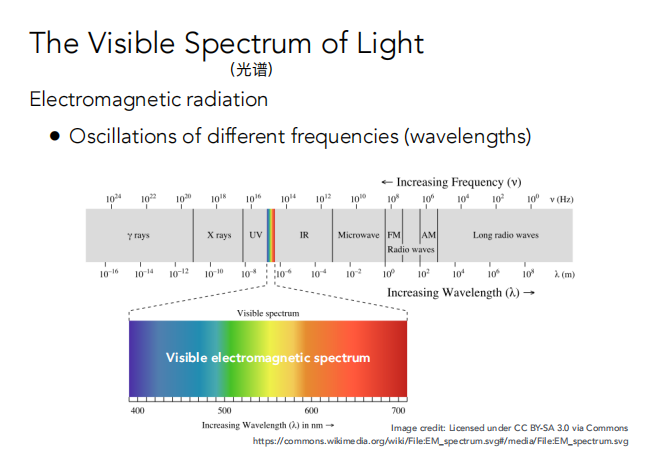
颜色是人的感知的结果，他不是光的自然属性。不同波长的光不是“颜色”。
2.1 颜色的物理学基础
2.1.1 可见的光的波段
2.1.2 谱功率密度 Spectral Power Distribution(SPD)
SPD 是光线不同波长的光强分布是多少，如下图所示蓝天能量集中在波长低的部分，日光波长越高能量越大。
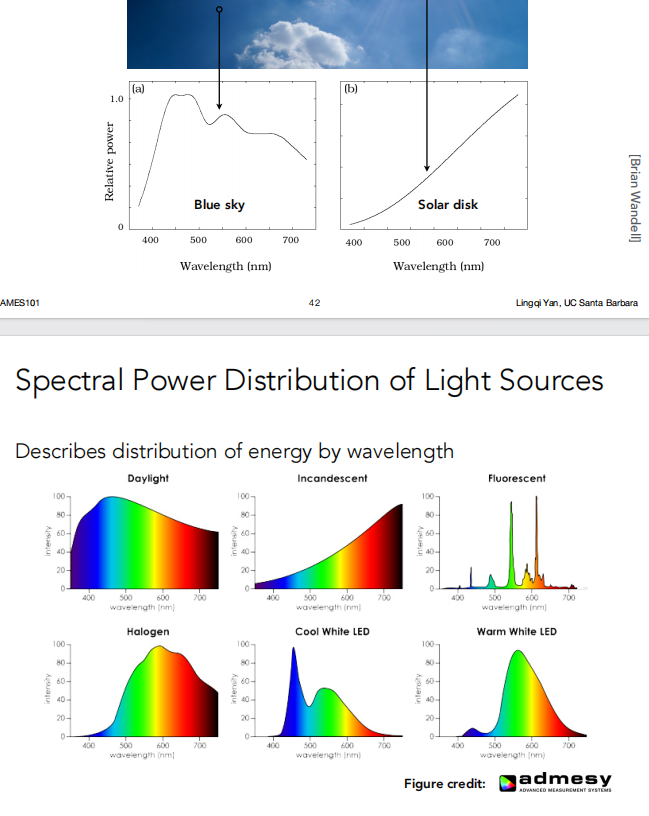
SPD 具有线性性质，即可以叠加。
2.2 颜色的生物学基础
人的眼睛是摄像机，瞳孔是光圈，晶状体是透镜（通过肌肉伸缩来控制焦距），视网膜是传感器。
2.2.1 感光细胞：Rods and Cones
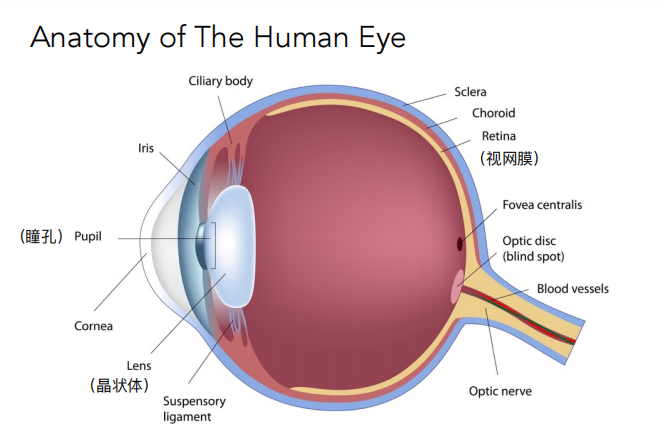
视网膜具有感光细胞（Retinel Photoreceptor Cells）：棒状和锥形细胞（Rods and Cones ）
Rods（棒状细胞）：感知光的强度，可以得到灰度图。~120 million
Cones（锥形细胞）：感知光的颜色。~6-7 million
由于三种类型的细胞对于波长的感光程度不同，Cones可以进一步划分为三类：S-Cone，M-Cone，L-Cone。
2.2.2 Tristimulus Theory of Color
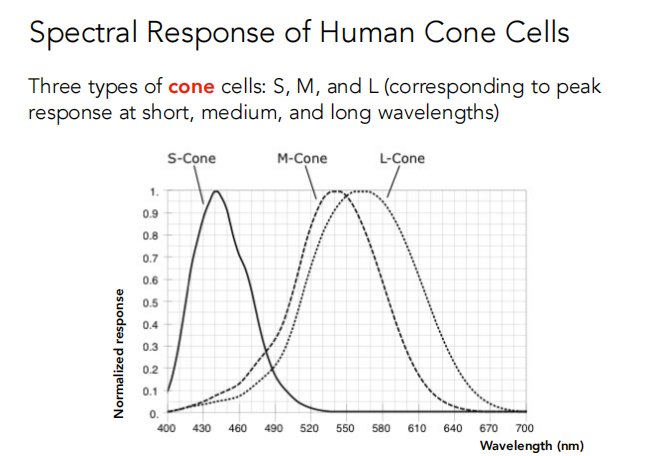
以下是人类锥形细胞的相应曲线，SML是人类最终看到的结果（只是一个数，不是光谱而是积分的结果）。
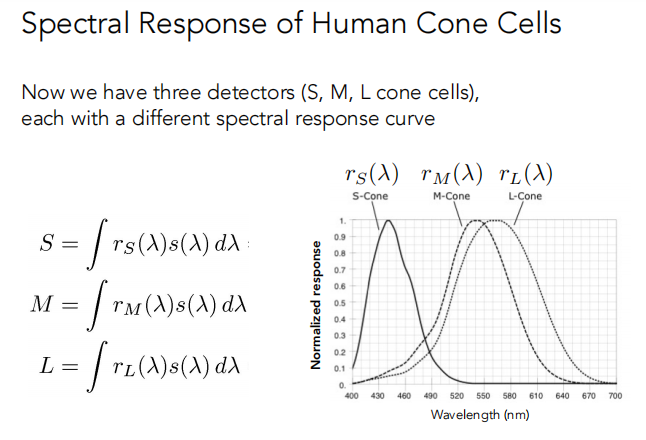
每一个光的波长信息不能被人眼测量和大脑接收。
眼睛值看到了三个 response values（S,M,L），并且是大脑唯一可获取的信息。
2.2.3 同色异谱（Metamerism）
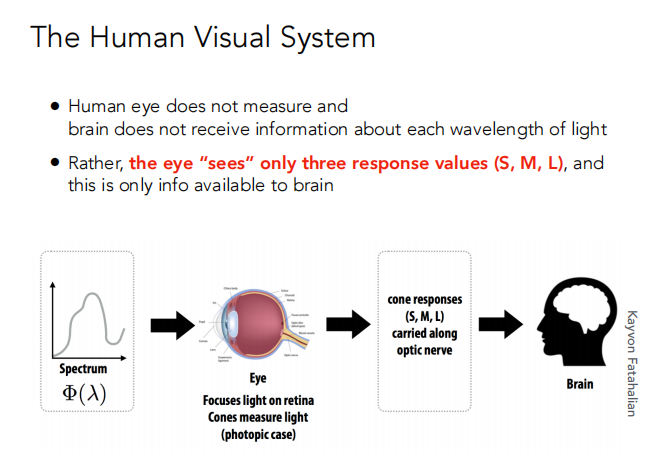
Metamerism 是不同的光谱 spectra（ ∞ − dim）会映射到相同（S,M,L）的响应。
- 这些似乎会对一个人产生相同的颜色（光谱不一定相同，但颜色可以相同）。
Metamerism 对颜色reproduction很重要。
- 不需要重构出真实世界的整个光谱。
- 例如metamer可以在显示器仅使用每个像素的三个颜色便可重现真实场景感知到的光。
2.3 颜色匹配（Color Reproduction / Matching）
加色系统 Additive Color
- 给定一组主要的光，每个光都有自己的光谱分布（例如使用RGB显示像素）。
- 调整这些光的亮度并把它们加在一起。
- 颜色最后被标量（R,G,B）描述。
（可以进行减色）
CIE RGB Color Matching
下图图显示每个CIE RGB主要（primary）光匹配x轴上给定波长的单色光需要混合的量。（注意有负的结果）。
对于任何一个光谱s，感知到的光被下面的公式匹配（缩放CIE RGB原色）。
2.4 颜色空间（Color Spaces）
2.4.1 Standard Color Spaces（标准颜色空间）
- 先让特定的机器做好之后，让其他机器模仿这种RGB标准。
- 现在被广泛采用。
- 色域gamut是有限的。
2.4.2 色域（Gamut）
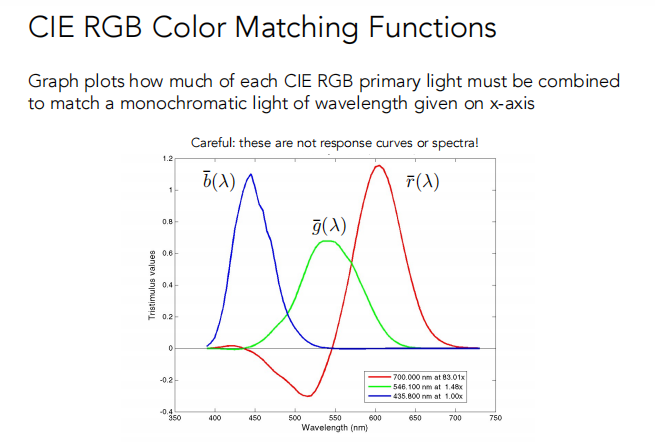
Gamut 是被一个原色集生成的所有色度（chromaticities）。
不同的颜色空间表示不同范围的颜色，具有不同的色域（gamut），即它们覆盖charomaticities的不同区域。
2.4.3 常见的颜色空间
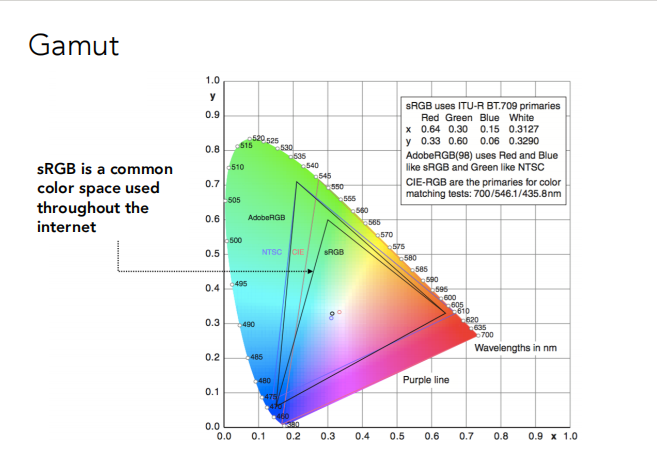
CIE是人造的颜色匹配系统。
首先设定标准颜色原色组X,Y,Z。
- 不存在具有这些匹配函数的原色。
- Y是luminace亮度（亮度与颜色无关）
这个系统设计成匹配函数严格为正，覆盖所有可见光的范围。
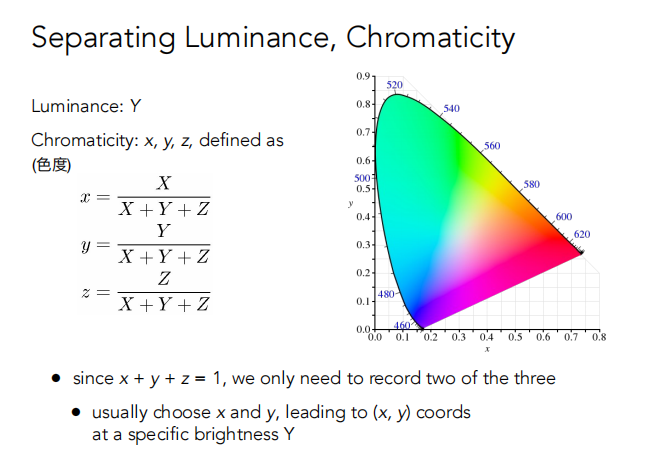
HSV 常见于颜色拾取器中（PS中常见）。
- Hue：不同类型的颜色。
- Saturation：更接近白色还是纯色（单一颜色）。
- Brightness：从黑色到某种颜色。
- CIELAB Space(AKA Lab*)
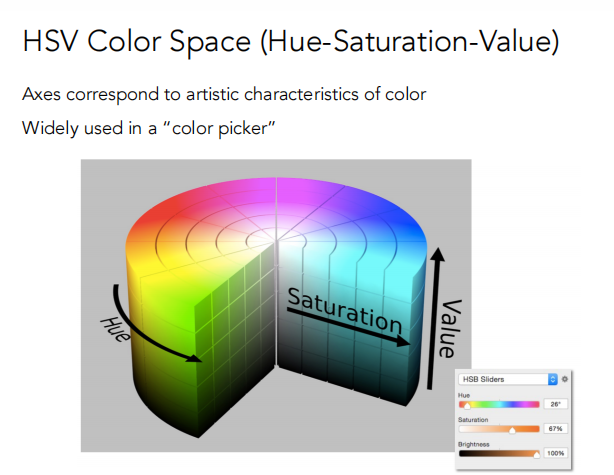
CIELAB Space是与感知有关的色彩空间。
- L* 是 Lightness（brightness）
- a 和 b 是互补颜色对（a是red-green，b是blue-yellow）。
- CMYK：A Subtractive（减色） Color Space
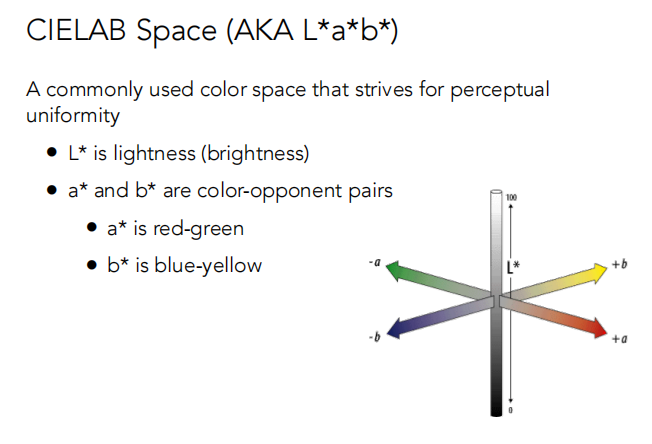
Subtractive color model：混合的越多就越暗。
青色Cyan、洋红Magenta、黄色Yellow和黑色，并（Key Widely）广泛用于打印。
【Games 101】Lec 19：照相机、镜头、光场
Lecture 19：Cameras, Lenses and Light Fields
1. 视场（Field of View（FOV））
1.1 概述
FOV：看到的角度
h：高度
f：焦距
1.2 焦距（Focal length）对视场（FOV）的影响
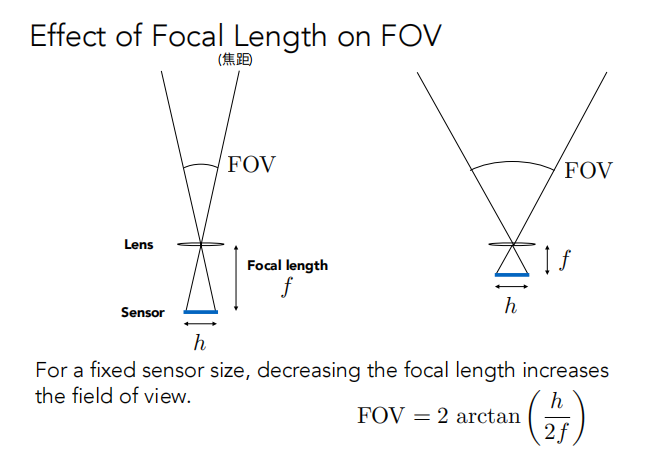
当传感器大小一定时，FOV 随着焦距增加而减少。
1.3 传感器（Sensor）大小对视场的影响
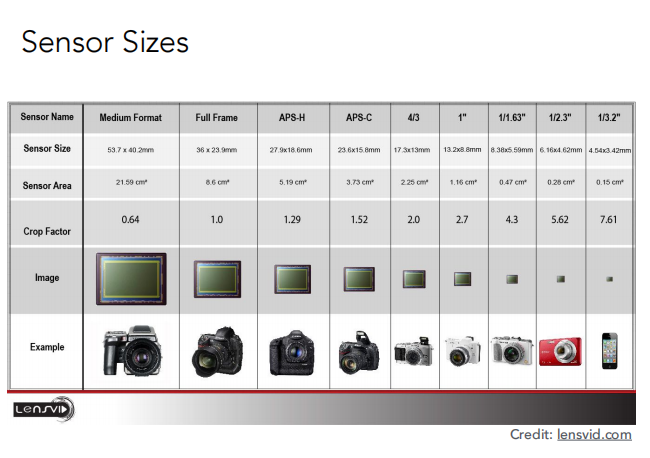
通常，相机（传感器）越大，镜头（焦距）越长越好。
2. 曝光 Exposure
2.1 概述
- H=T×E
- Exposure = Time × Irradiance
- T（曝光时间）由快门（shuttle）控制
- E（Irradiance）由传感器上一个单位区域接收光的能量和镜头的光圈（aperture）和焦距控制。
2.2 曝光的影响因素
- Aperture size（光圈的大小）：通过打开和关闭 apeture 改变 f-stop。
- Shuttle speed（快门开放的时间）：改变sensors的曝光时间即每个像素接收光的时间，快门越快曝光越少
- ISO （Gain 感光度）：更改传感器值和数字图像值之间的倍率（模拟和/或数字）。
2.3 感光度 ISO（Gain）
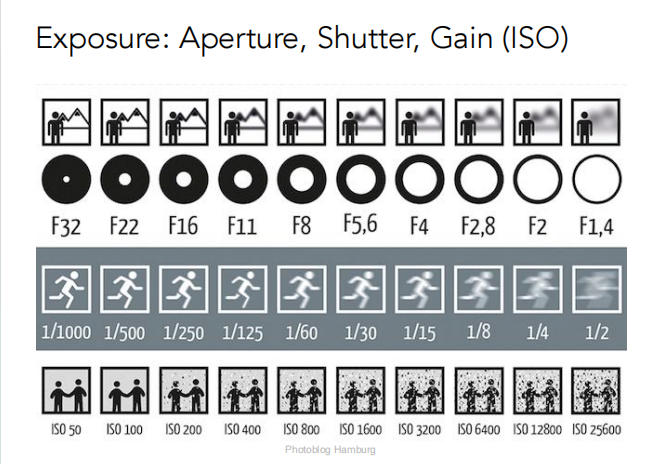
ISO 是 exposure 的第三个变量，简单放大ISO信号的同时会方法噪声。
Film：权衡对（grain）的敏感度。
Digital：权衡对噪声的敏感度。
- 在模拟到数字的转换前乘以信号。
- 线性作用（ISO 200需要的光是ISO 100的一半）
2.4 F-Number(F-Stop)：Exposure Levels
- 用于描述光圈的
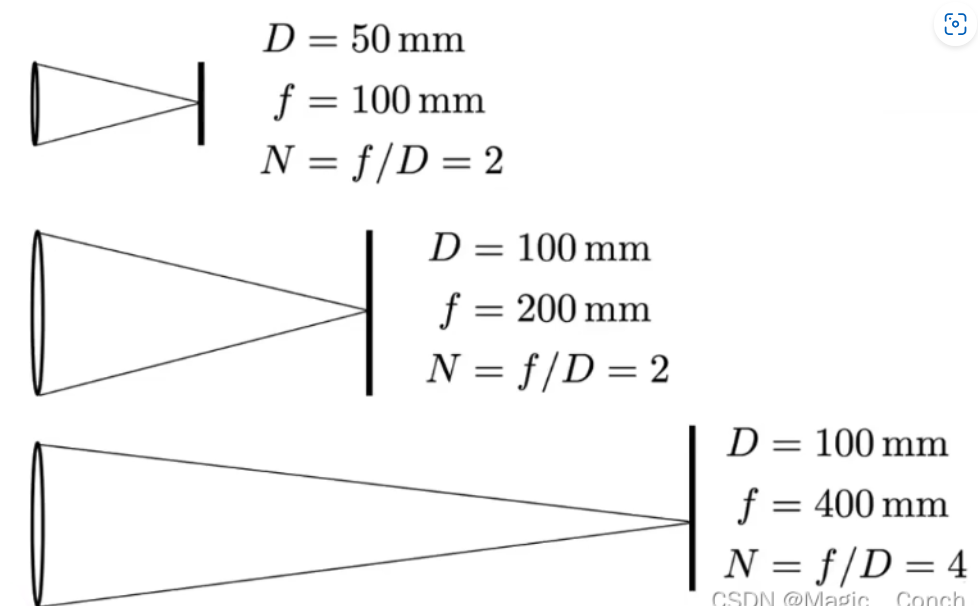
写作 FN或F/N，N就是f-number。
简单理解为光圈的直径的倒数。
正式定义：镜头的 f-number 是 焦距 除以 光圈的直径。
2.5 快门 Physical Shutter
快门可以用于调节曝光度。
运动模糊（Motion blur）：由于快门打开有时间会拍摄到一段运动。
两倍的快门时间意味着两倍的运动模糊。
运动模糊不一定是坏事，从人的感知角度它可以形容速度快从采样角度，它也可以进行反走样。
Rolling shutter：图像上的不同位置可能会记录不同时间进入的光（会造成扭曲）。
2.6 F-Stop vs Shutter Speed
两者可以组合，调节曝光度；
Photographers 需要权衡景深和运动物体的运动模糊。
2.7 高速摄影和延时摄影（Fast and Slow Photography）
High-Speed Photography：每秒拍更多的照片，也导致快门时间很少（短曝光时间，得用更大的光圈）。
Long-Exposure Photography：长曝光时间，小光圈。
3. 薄透镜近似 Thin Lens Approximation
真正的透镜非常复杂，需要一个简单的方法描述。
3.1 理想化薄透镜（Ideal Thin Lens - Focal Point）
- 所有进入透镜的平行光一定过焦点。
- 过交点的在透镜后面一定是平行光。
- 认为焦距可以被随意改变（透镜组）。
3.2 薄透镜公式（The Thin Lens Equation）
- 公式：（物距，像距，焦距 三者的关系）
- 公式推导：
3.3 Defocus Blur
3.3.1 Computing Cicle of Confusion(CoC) Size
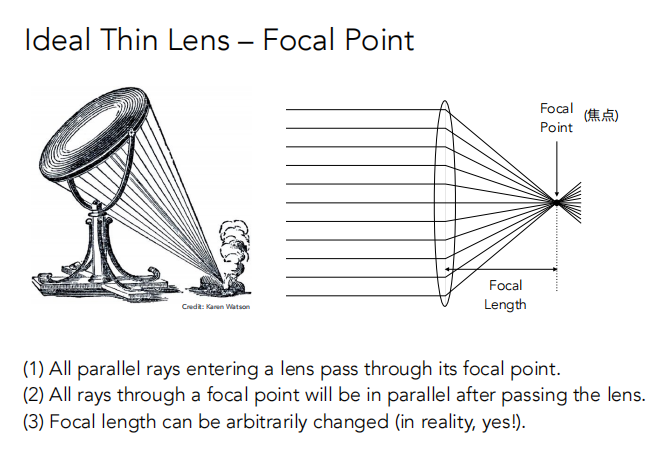
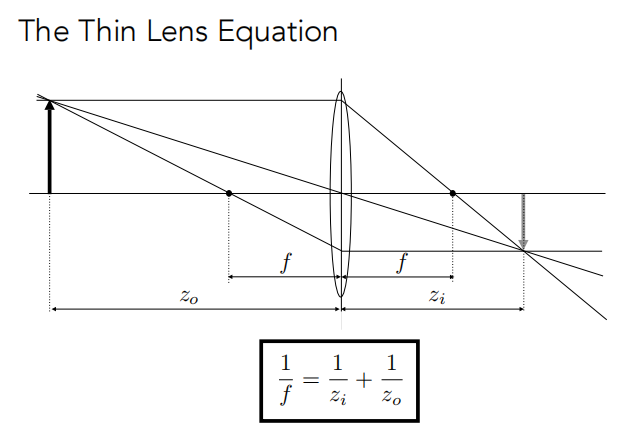
如图，Object远离Focal Plane，聚焦后的点不在Sensor Plane上，而是在它前面聚焦，然后光线在聚焦点继续直线传播，到Sensor Plane上就变成了一个圆。（产生了模糊）
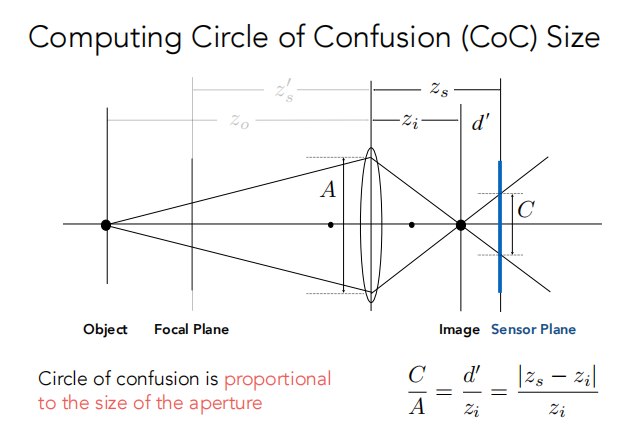
其中：A是光圈直径，C是CoC的直径。
Circle of Confusion 与光圈大小成正比。所以看到的东西是否模糊与光圈的大小有关。
将上面的公式与F-Number联系起来。
3.3.2 Ray Tracing Ideal Thin Lenses
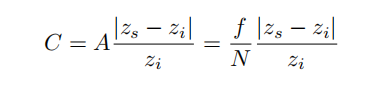
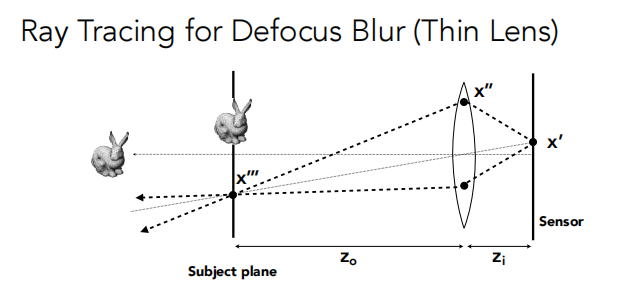
步骤：
- 先定义Sensor的大小（成像平面大小），然后定义透镜的属性，即焦距和光圈的大小。
- 定义透镜和关注平面的距离 zo（物距）。
- 根据透镜方程计算相应的深度 zi（相距）。
渲染：
- 对于每个在sensor上的像素 x′
- 在 lens plane上取样随机一点 x′′
- 然后知道了通过透镜的光线会打到 x′′′
- 计算光线 x′′ → x′′′ 的radiance。
3.3.3 景深（Depth of Field）
景深：就是指 成像清晰的一段范围
或者说：在场景内对应的CoC足够小的距离范围。
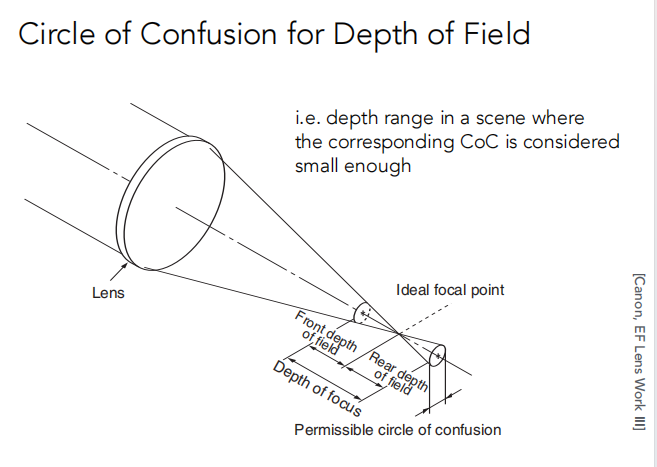
推导：
参考
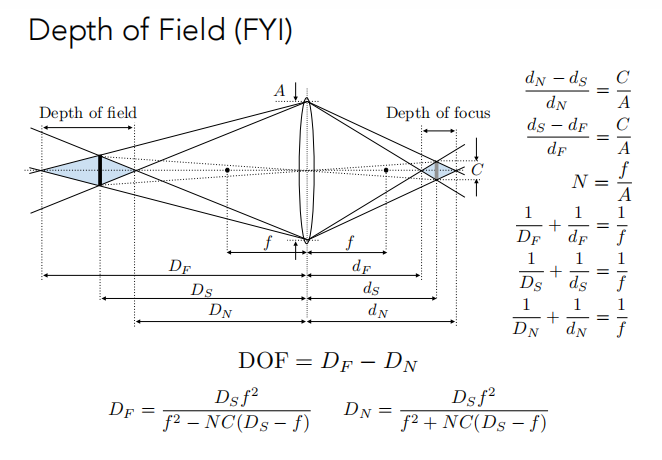
图形学笔记（十七）相机，棱镜 ——FOV、焦距、曝光、F-Stop、ISO、薄透镜公式、Circle of Confusion Size、景深、理想薄透镜光线追踪_相机凌镜成像-CSDN博客
光场放在了下一篇。
【Games 101】Lec 18：渲染的前沿话题
Lecture 18：Advanced Topics in Rendering
东西很多，当作扩展听一听就行。
1. 高级光线传播
1.1 概述
- 无偏光线传播
- 双向路径追踪
- Metropolis light transport (MLT)
- 有偏光线追踪
- 光子映射
- Vertex connection and merging (VCM)
- 试试辐射度算法
1.2 有偏（Biased）与无偏（Unbiased）的 Monte Carlo 估计
- 无偏
- 无偏的 Monte Carlo方法没有任何系统误差。即无论使用多少样本，无偏估计的期望值总是正确的。
- 有偏
- 有系统误差存在就是有偏估计。
- 有偏估计的一致性（consistent）：当取样无穷大时没有系统误差（会收敛）
在图形学中
- Biased（有偏） == blurry（模糊）
- Consistent（有偏一致性） == 当取样点无穷时不模糊
1.3 双向路径追踪 Bidirectional Path Tracing（BDPT）
1.3.1 概述
- 无偏的 光线传播方法。
（路径追踪是从相机到光源使用一条路径连接起来。）
1.3.2 BDPT 思想
- 分别从相机和光源追踪sub-paths
- 从两个 sub-path 连接端点（各追踪一部分然后汇聚）
1.3.3 BDPT 特点
- 适合光线传播在光源这一边比较好算的情况。
- 难以实现且非常慢
1.4 Metropolis Light Transport （MLT）
1.4.1 概述
- 无偏估计
- 用马尔可夫链来进行采样
1.4.2 马尔可夫链 Markov Chain Monte Carlo（MCMC） application
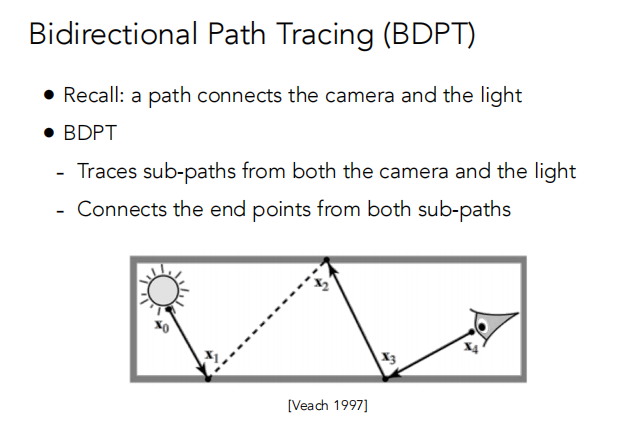
根据当前的样本可以生成与其靠近的下一个样本，他可以生成以任意形状函数为PDF的样本。
关键思想：局部扰动一个现存路径来获得一个新路径。
1.4.3 特点
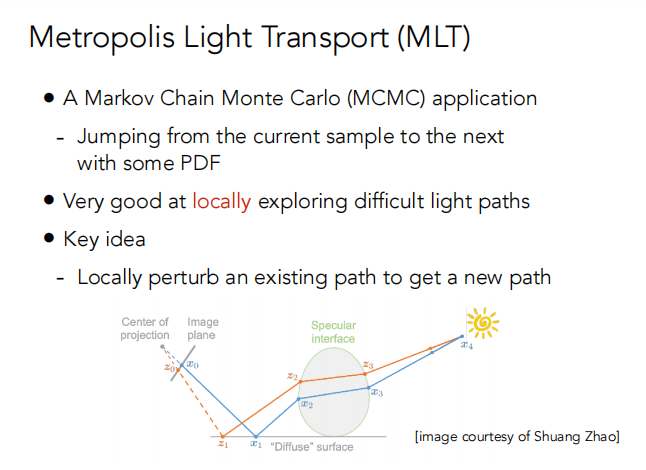
优点：
- 比较适合做困难的光线传播（只要找到一条路径做为种子就可以找到更多路径）
- 无偏
缺点：
- 难以估计收敛速度
- 不能保证每个像素的收敛速度都相等（比较局部）
- 所以图片看起来比较脏
- 不能渲染动画
1.5 光子映射（Photon Mapping）
1.5.1 概述
- caustics（聚焦）：由于光线聚焦产生的一些列图案。
- Specular-Diffuse-Specular（SDS）：光线先通过镜面反射，然后再进行漫反射，然后再进行镜面反射。
- 有偏的
- 擅长处理 Specular-Diffuse-Specular（SDS）paths 和生成 caustics。
1.5.2 方法
- 光子追踪
从光源发射光子，让它们在四周弹射，直到光子打到diffuse的物体上，把光子记录下来。
- 光子收集
从眼睛和摄像机开始，射出 sub-paths，让它们在周围跳跃，直到它们打到漫反射的物体上。
- 计算局部密度估计
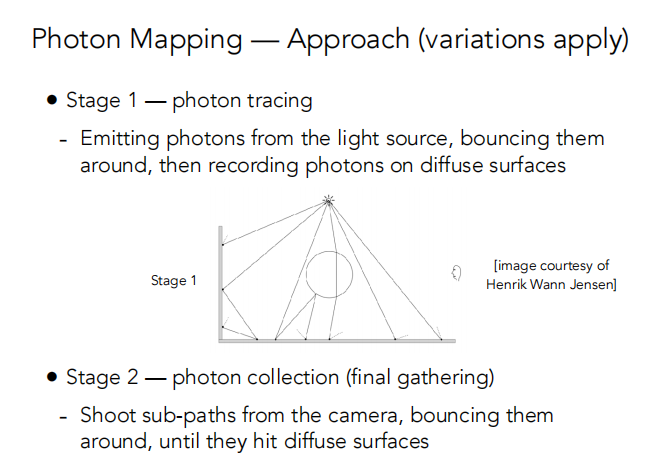
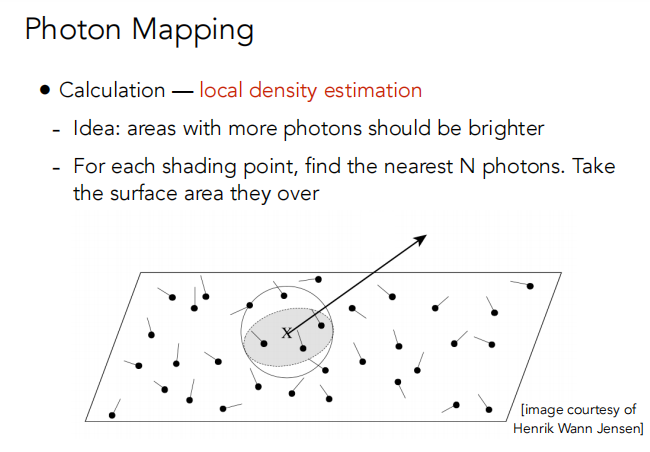
当第二趟打到 diffuse 物体表面时，就要做一个局部的密度估计。
思想：光子分布越集中越亮。
做法：对于每个着色点，找到最近的N个光子。计算它们占据的面积。然后就可以计算光子的密度。
1.5.3 分析
为什么有偏？
- 密度的估计不准确，只有 dA 足够小才接近正确。
解决
- 更多的光子辐射出去 → 相同的N个光子则会覆盖更小的区域 ΔA → ΔA 会更加接近 dA。所以它是biased，但是 consistent 的。
1.6 顶点连接和合并 Vertex Connection and Merging（VCM）
1.6.1 概述
结合了 双向路径追踪 和 光子映射
1.6.2 思想
- 如果端点不能被连接而是可以被融合就不浪费 BDPT 中的 sub-paths了。
- 使用 photon mapping 来处理 “photons” 附近的融合。
1.7 实时辐射度算法 Instant Radiosity (IR)
- 也称为 many-light 方法
- 思想：已经被照亮的表面可以被当作光源。
- 方法：
- 从光源打出 sub-paths 并把每一个 sub-path 的端点当作 Virtual Point Light（VPL）
- 使用这些 VPLs 渲染场景
- 优点：快速并且通常对漫反射场景的结果比较好。
- 缺点：
- 当 VPLs 非常接近着色点的时候，Spikes 将会融合（如下右图有过亮的点）。
- 不能处理glossy的材质。
2. 高级外观建模
2.1 非表面材质
2.1.1 散射介质（Participating Media）
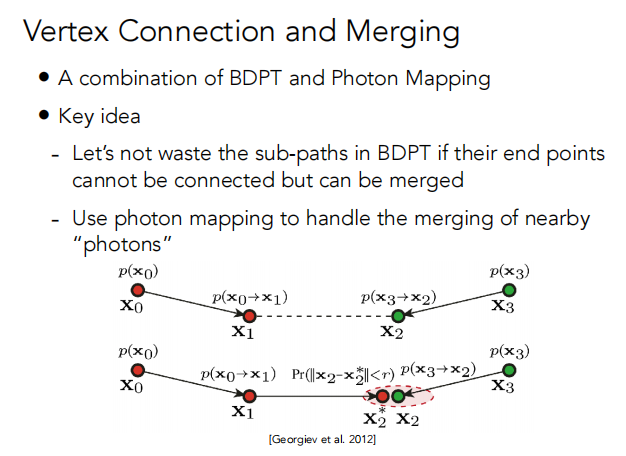
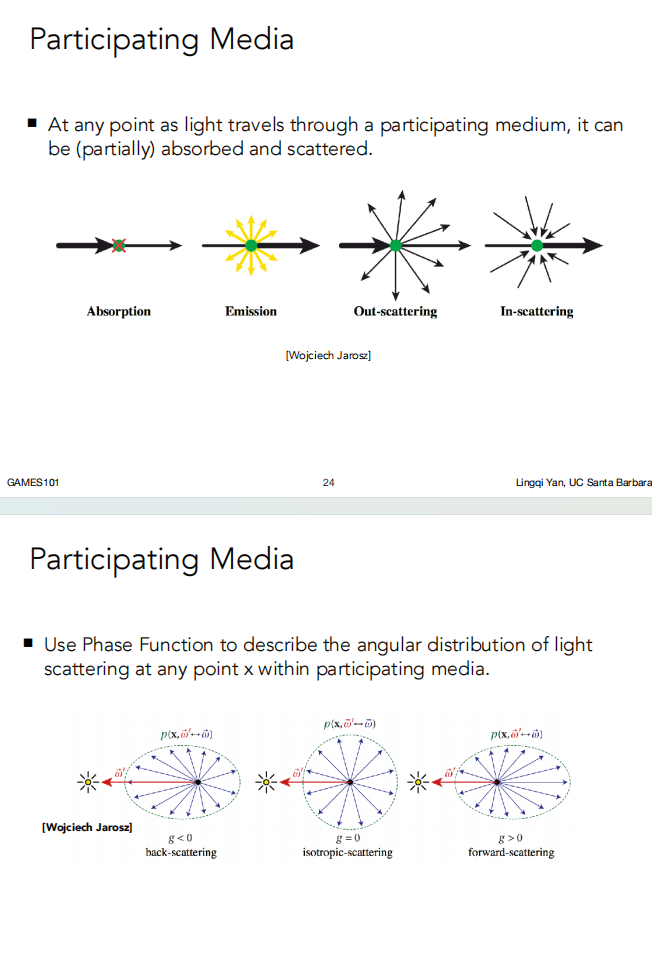
当光通过散射介质时，任何一点可以(部分)吸收和散射。
使用相位函数（Phase Function）来描述参与介质中任意点的光散射角分布。
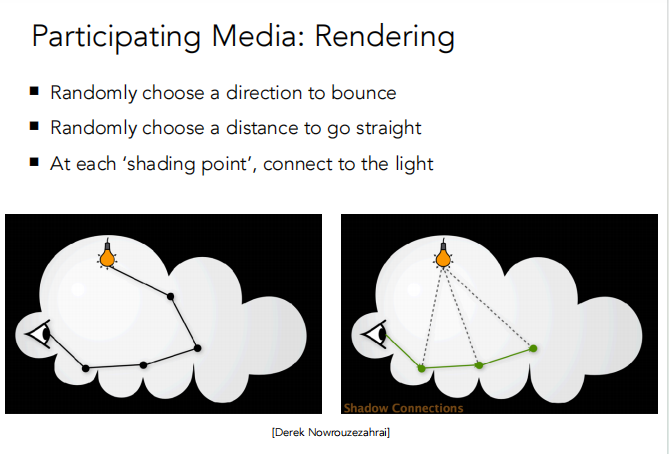
散射介质的渲染过程
- 随机选择一个方向来弹射。
- 随机选择一个距离直行。
- 对于每一个“着色点”，把它连接到光源。
2.1.2 Hair Appearance
- Kajiya-Kay Model
头发会散射成一个圆锥。像是diffuse+specular。
- Marschner Model
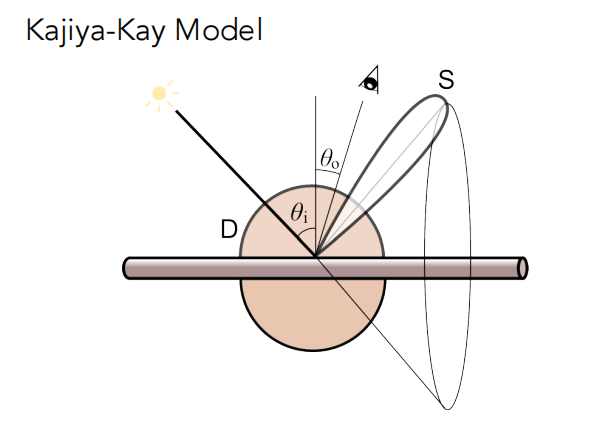
除了考虑被散射的光线还要考虑穿过头发的光线。Marschner Model 考虑了以下三证类型的光线。
R：直接反射的光。
TT：穿进去再传出去的光。
TRT：光线进到头发里面，在头发的内壁发生一次反射再回去。
2.1.3 Fur Appearance
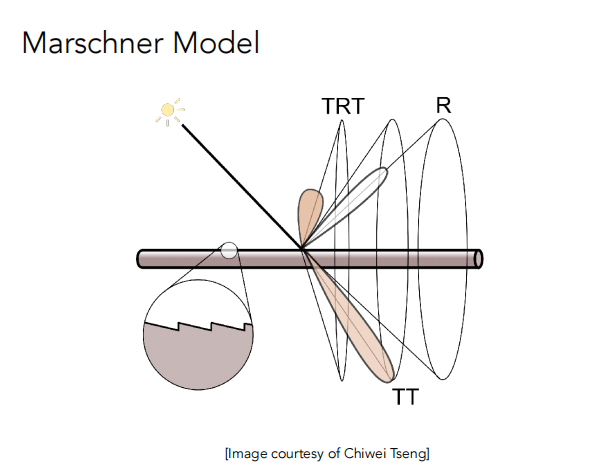
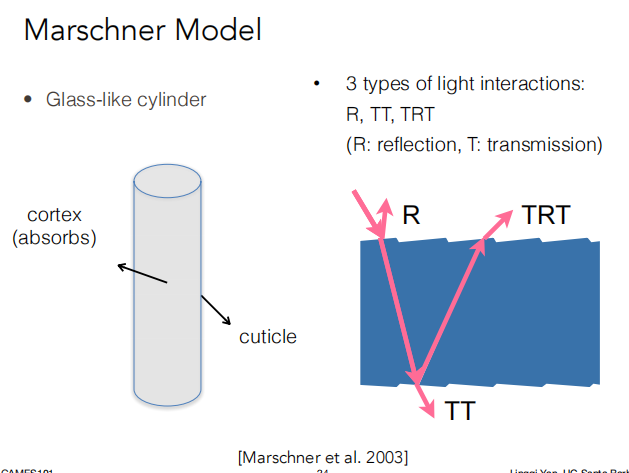
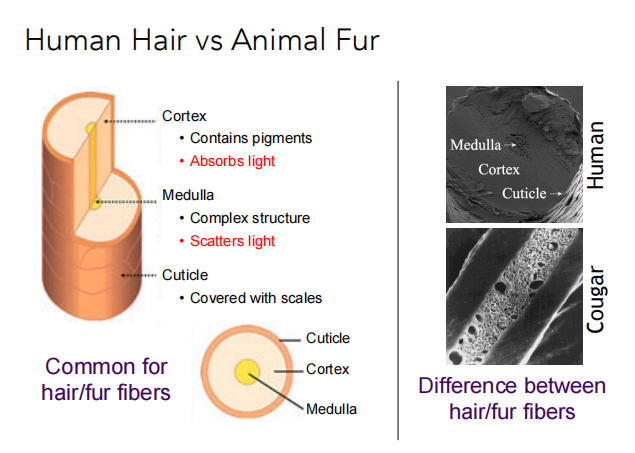
人和动物毛发都具有三层结构，如下图所示。但动物的 Medulla 比人大很多。
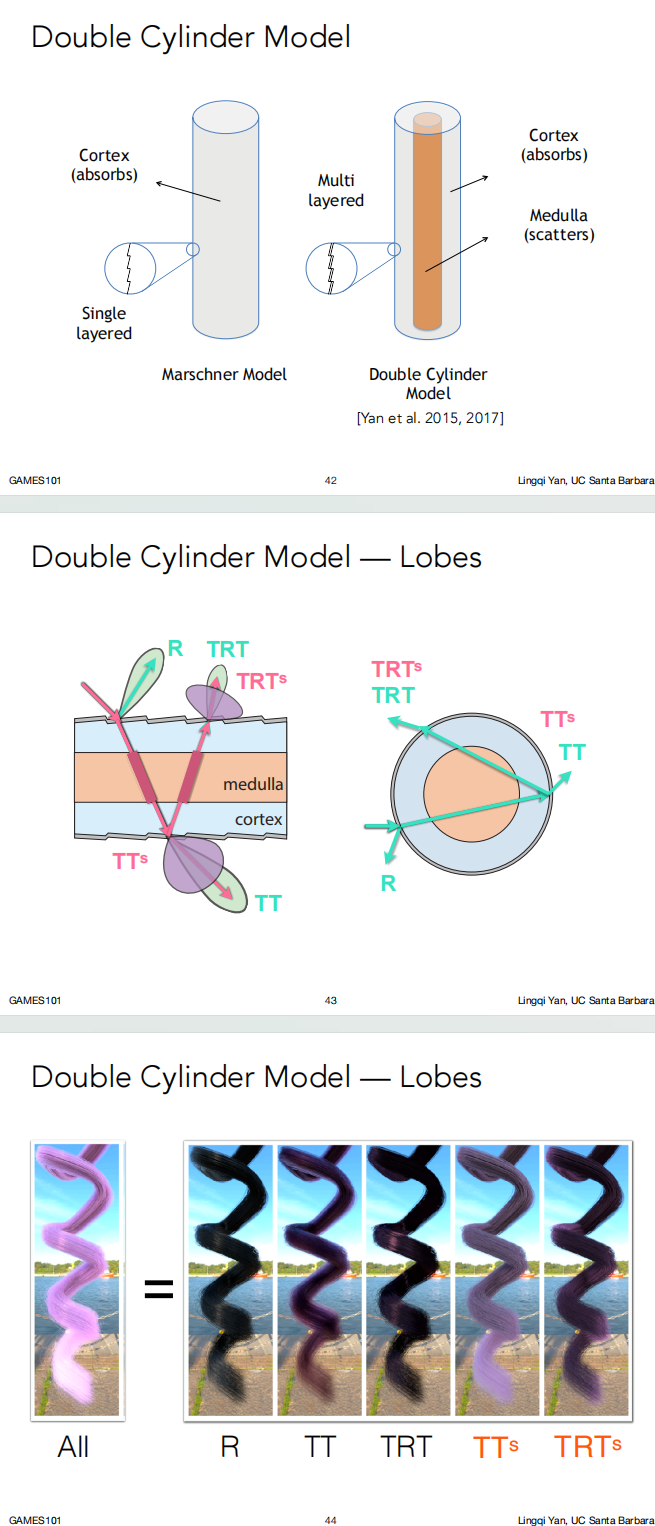
双层圆柱模型 Double Cylinder Model
2.1.4 颗粒材质（Granular Material）
2.2 Surface Model
2.2.1 Translucent(半透明) Material
2.2.2 次表面散射（Subsurface Scattering）
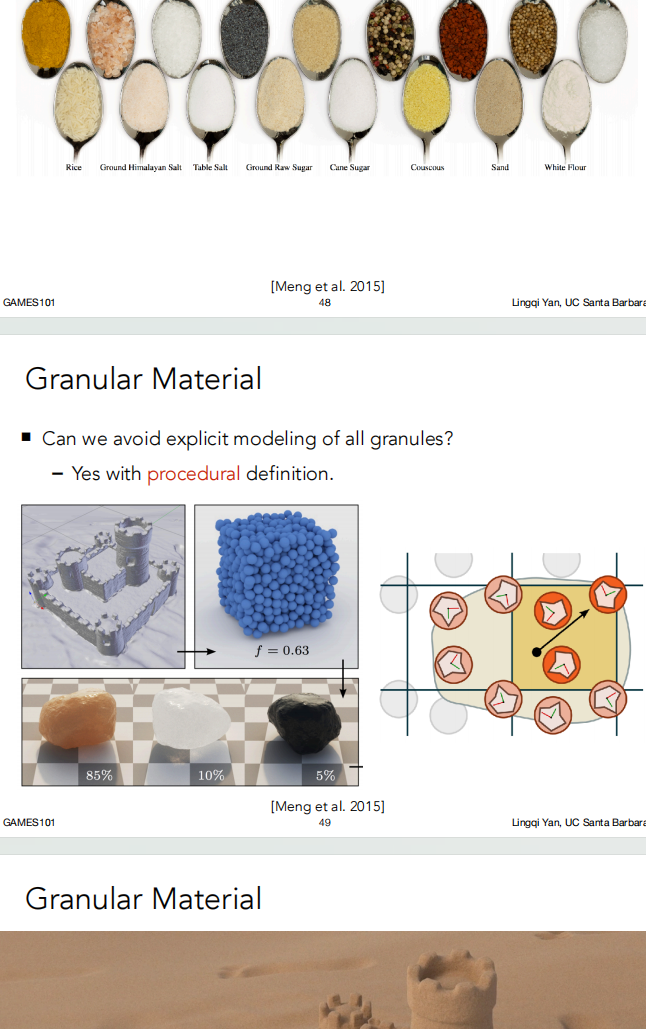
Subsurface Scattering 是在表面下发生的散射。
- BSSRDF 是BRDF概念的延申。它表示某一点的出射radiance来源于另一个点的微分irradiance。
- Scattering Function 渲染方程的延申，表示所有表面上的点和所有方向的积分。
- Dipole Approximation 通过引入两个点光源来近似次表面散射的效果
2.3 布料 Cloth
2.3.1 概述
- 布料是一系列缠绕的纤维构成的。
- 缠绕有两级：纤维（Fiber）第一次缠绕会成为股（Ply），股（Ply）缠绕会成为线（Yarn）。
2.3.2 渲染布料的三种方式
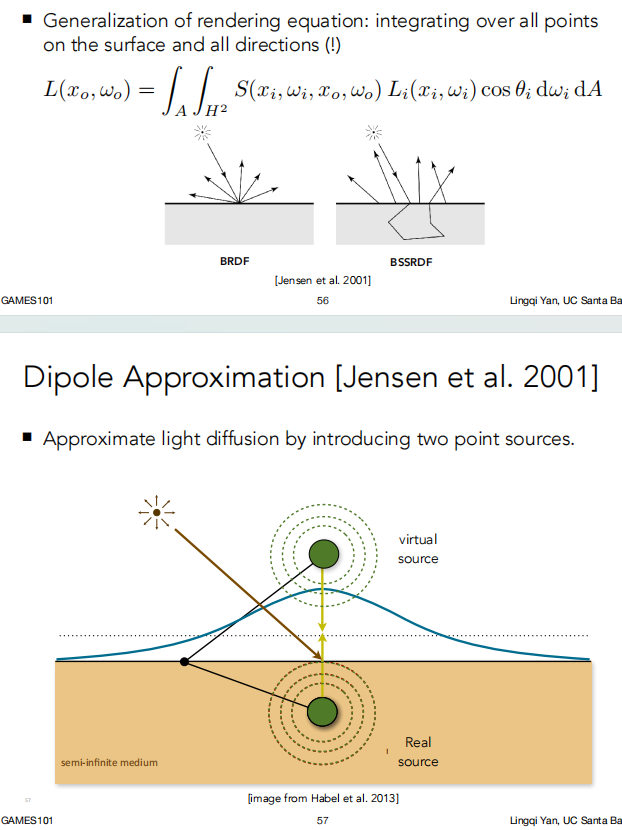
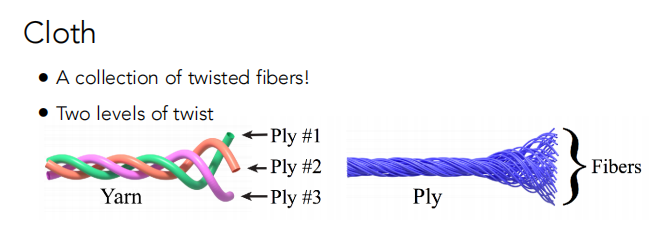
Cloth: Render as Surface（把布料当作表面来渲染）
- 给定编制图案，计算总体表现。
- 使用BRDF来渲染。
- 但是对于天鹅绒，根本不是一个平面，所以当作表面来渲染不合理。
Cloth: Render as Participating Media（把布料当作散射介质来渲染）
- 把单个纤维和它们分布的性质转化为散射参数。
- 然后把它们当作散射介质来渲染。
Cloth: Render as Actual Fibers （把布料当作真实的纤维来渲染）
- 即明确的渲染每一根纤维。
2.4 Detailed Appearance
2.4.1 动机
渲染出来的太过“完美”，而真实的世界中充满着各种各样的细节。
而细节很难通过渲染表现出来。
因为对于微表面模型来说，通过从光源的不断反射，只有非常少的一部分会被反射到相机。
2.4.2 解决：BRDF over a pixel
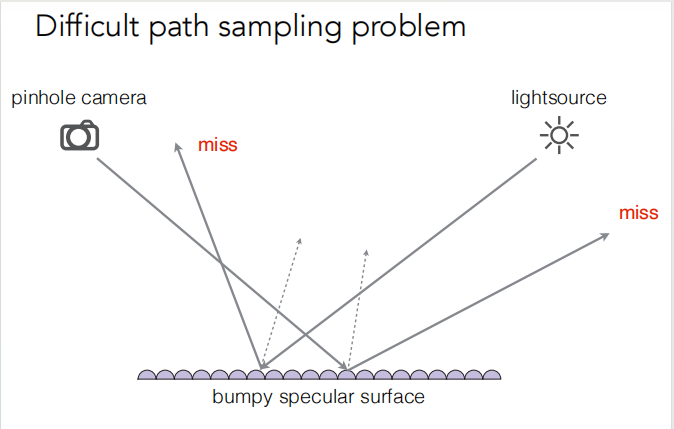
由于像素覆盖很多的微表面，所以将一个像素覆盖的法线分布计算出来然后替换光滑的法线分布，用在微表面模型里。
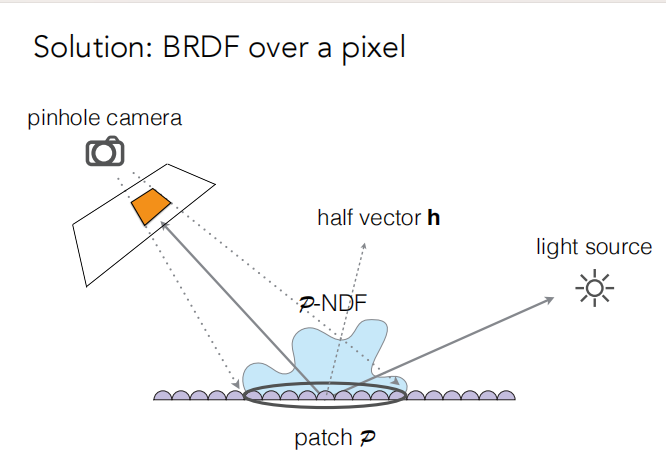
一个可以像素覆盖不同大小的微表面，对于比较大的范围会得到统计学规律，而对于比较小的微表面得到的就比较有特点。
不同类型的法线贴图会得到不同的法线分布。
2.5 波动光学
当物体非常小，就不能假设光沿直线传播，而是要考虑波动性，考虑光的波动性。
波动光学的 BRDF 与几何相似，但是相对而言比较不连续。
2.6 程序化生成的外观（Procedural Appearance）
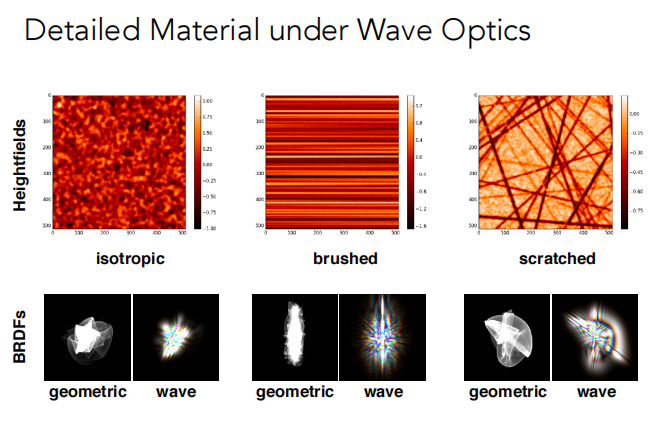
动机 不使用纹理贴图来定义细节。
3D noise（噪声函数）： 可以直接通过噪声函数来计算细节，使用这种方法可以看到被切割或断裂的内部纹理。
应用：地形、水面、木头。
参考
图形学笔记（十六）渲染的高级问题 —— BDPT、MLT、光子映射、VCM、IR、散射介质、毛发材质（双圆柱模型）、次表面散射、布料渲染-CSDN博客
这周事情比较多，人又懒得一批… 就一直没更…
【Games 101】Lec 17：材质和外观
Lecture 17：Materials and Appearances
1. 外观和材质
外观是光照和材质共同作用的结果。
由于材质不同，光线作用后会得到不同的结果，同样的模型会渲染出不同的结果。
渲染方程中，由BRDF来决定材质。所以，Material == BRDF
2. 反射和折射
2.1 完全镜面反射（Perfect Specular Reflection）
对于完全镜面反射，有两种辨别方法：
- 入射光方向 = 出射光方向，它们中间是法线。
- 把角度投影到局部坐标系，从上往下看，入射角和出射角相反。
反射方向的计算方法：
2.2 折射（Specular Refraction）
2.2.1 折射定律（Snell’s Law）
由折射定律，η 是不同材质的折射率，有：
投影后满足下面的关系：
如果入射介质的折射率 大于 折射介质的折射率 就会发生 全反射。
折射定律公式：
2.2.2 Snell’s Window / Circle 现象
由于全反射现象，从空气打到水面的光线超过一定角度就无法进入人眼，形成了下面的Snell’s Window / Circle 现象。
2.3 菲涅尔项（Fresnel Reflection / Term）
2.3.1 概述
反射 和 入射光的角度有关。
比如上面图片中，当入射光线（我们的视线）和桌子的法线越垂直，反射就越明显；
不同的材质他们的效果是不一样的，比如镜子，那么不论从哪个角度看，反射都很明显；
这个材质的性质，我们用菲涅尔项来定义；
下面这个菲尼尔项是上面例子的：可以看到角度越大反射率越高
2.3.2 Fresnel Term 公式
- 精确公式：需要考虑极化（polarization）
- 近似公式：Schlick’s approximation
3. 常见材质
3.1 漫反射材质（Diffuse / Lambertian Material）
在漫反射中，光被到达后会被均匀的反射到四面八方。
现在假设进来的光也是均匀的，即来自各个角度的 Irradiance 是相同的。那么如果表面不吸收光，那么入射和出射的 Irradiance，且入射和出射都是均匀（uniform）的，那么入射光和出射光的 Radiance 也是相同的。
漫反射的 BRDF 推导如下：
- 其中 ρ 是反射率；
- 如果是完全不吸收能量，即反射率 ρ = 1，此时 BRDF = 1 / π
3.2 Glossy material（BDRF）
Glossy material是被打磨的铜镜之类的材质效果，是较为模糊的镜面，BRDF 的反射方向集中在一个小范围内。
3.3 Ideal reflective / refractive material(BSDF*)
此种材质同时具有反射和折射，可以使用BSDF来表示这种材质（同时考虑反射和折射）。
BSDF = BRDF + BTDF
3.4 微表面材质（Microfacet Material）
3.4.1 概述
基本思想：
- 如果离一个物体足够远，那么就看不到表面的细节，取而代之的是表面上的物体对表面的作用，即对光总体的效应。
例子：
- 如下图太阳找到澳大利亚，澳大利亚的不同地形反映出来的是一个比较亮的材质。
3.4.2 微表面原理（Microfacet Theory）
微表面模型认为从远处看到的是材质外观，从近处看到的几何。
关键 研究微表面法线的分布。如下图所示，不同的法线分布会产生不同的材质：
- 法线分布集中就是 Glossy；
- 分散就是 Diffuse。
3.4.3 Microfacet BRDF（微表面的BRDF）
Microfacet BRDF主要由三项构成：
- Fresnel term：不同入射方向带来不同程度的反射，侧重能量。
- distribution of normals：法线分布，表示对于给定方向分布的值是多少。结合半程向量h就可以确定什么样的微表面可以从入射反射到出射（半程向量离法线越近越能反射）。
- shadowing-masking term：几何项，由于自遮挡现象使得有些微表面的作用。当光线几乎平着的打到微表面就容易发生shadow-masking。
3.5 各项同性/各向异性材质（Isotropic / Anisotropic Material (BRDFs)）
3.5.1 概述
各向异性会产生如下效果。
关键：各向异性的表面的法线分布具有方向性。
3.5.2 各向同性与各向异性的区别
区别：如果BRDF不满足在方位角上旋转得到的还是相同的BRDF，则称为是各向异性材质。
简单来说各向同性的 BRDF 只和相对的方位角有关，而各向异性材质不止和相对方位角有关还和绝对方位角有关。
4. BRDFs 的性质
- BRDF 是非负的：
- BRDF 是线性的，可拆分：
- BRDF 具有可逆性（Reciprocity）：交换入射方向和出射方向的角色，得到相同的 BRDF。
- BRDF 能量守恒：
- 各向同性与各向异性：
5. 测量 BRDFs
只有测量出的 BRDF 才是真正的 BRDF。
5.1 动机
- 避免计算 BRDF 模型，只要测量出来就可以用。
- 计算的不一定准确，但测量能准确的得出真实世界的材质。
5.2 测量方法
测量 BRDF 就是让光影和相机从各个方向去照去拍。
下图是测量工具：gonioreflectometer，可以精确到0.1°的级别。
5.3 伪代码和优化
伪代码：
1 | foreach outgoing direction wo |
优化：
- 各向同性把维度从 4 维减少到了3维
- 使用可逆性减少了一般的测量
- 使用更加巧妙的光学测量
5.3 表示 BRDF
5.3.1 要求
- 紧凑的表示
- 测量数据的准确表示
- 对随意一对方向的高效预测
- 可用于重要性抽样的良好分布
5.3.2 表格化表示（Tabular Representation）
把规则空间采样存储到三维数组 ( θi , θo , ∣ ϕi − ϕo ∣) 里。
参数化角度以更好地匹配镜面反射。
一般需要将测量值重新采样到表格中。
参考：
图形学笔记（十五）材质和外观 —— 菲涅尔项、常见材质（微表面材质、各向同性与各向异性）、BSDF、BRDF的性质、测量BRDF-CSDN博客
好多好难…
【Games 101】Lec 15：光线追踪 3（辐射度量学，光传输，全局光照）
Lecture 15：Ray Tracing 3 (Light Transport & Global Illumination)
这节课讲的是 Light Transport & Global Illumination 当然首先包含了上一节课最后的辐射度量学；
ps：这几节课是真的难…
1. 辐射度量学（Basic radiometry）
1.1 概述
辐射度量学的动机：
光源中定义L=10，但是10代表的是什么无法确定，缺少单位。
定义：
辐射度量学就是在物理上准确度量光照的方法。
它定义了一系列的方法和单位，准确的定义了光在空间中的属性：
- Radiant flux（辐射通量）
- intensity（辐射强度）
- irradiance（辐射[照]度）
- radiance（辐[射]亮度）
1.2 角，立体角（solid angle），微分立体角
- 角 Angle： 圆上的弧长与半径的比值。
- 立体角（solid angle）：球面上的面积和半径平方的比值。（弧度制在三维空间的延申）
- 微分立体角（Differential）
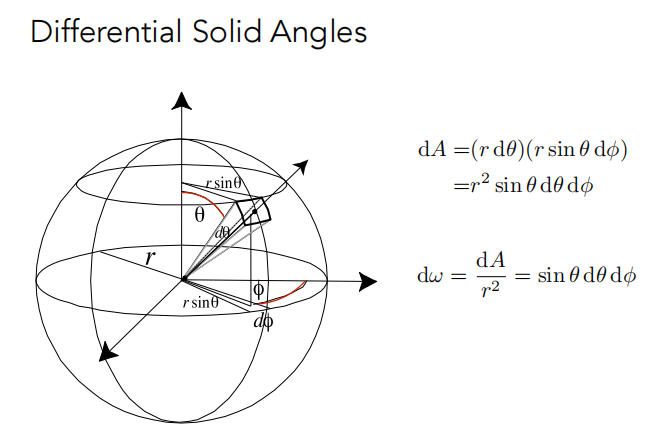
dA 是球面上的微分面积，近似成长方形
通过积分可以得到，整个球的立体角是 4π 。
1.3 Radiant Energy and Flux (Power)
1.3.1 Radiant Energy
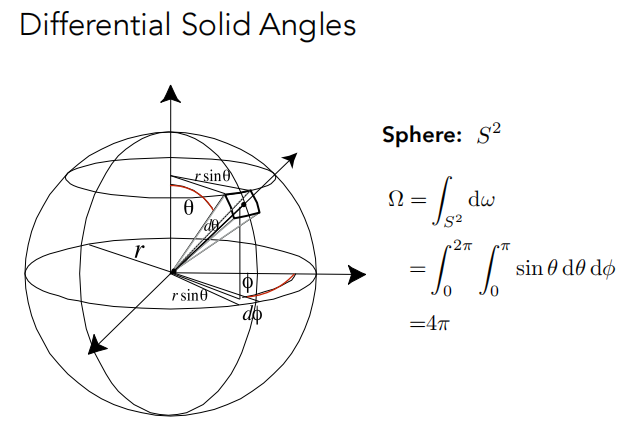
定义：Radiant energy是一种电磁辐射的能量。它由 焦耳（J=Joule）单位来度量，用符号Q来表示。
1.3.2 Radient Flux(Power)
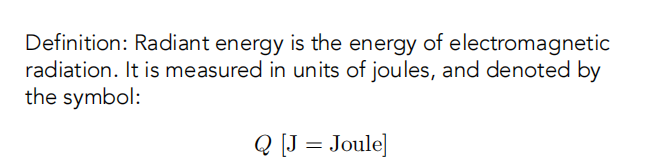
定义：
- Radient flux(Power) 是单位时间的发射出的、反射的、传播的和接收的能量。
- 或者：单位时间辐射出光子的数量
1.4 与光相关的物理量
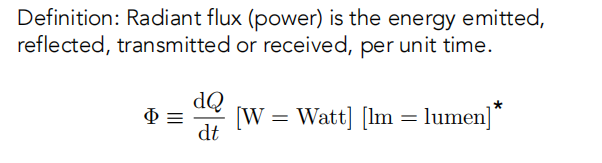
主要是区别下面三种物理量：
- Radiant Intensity：光源辐射出的能量；
- Irrdiance：物体表面接收的光的能量；
- Radiance：光线在传播过程中的能量；
1.4.1 Radient intensity
定义：
- Radient intensity是 每单位立体角 辐射的能量。
1.4.2 Irradiance
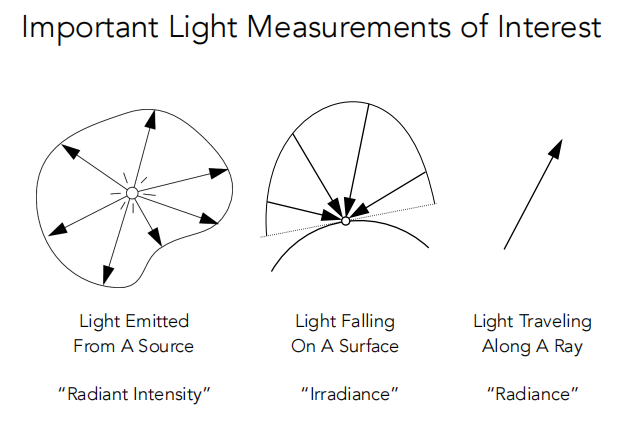
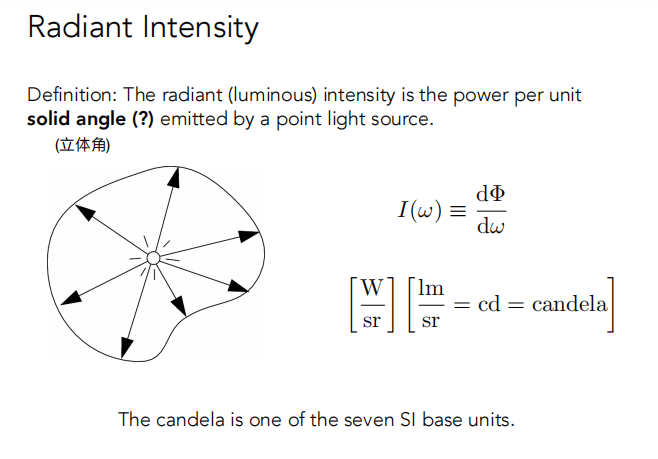
定义：
- Irradiance 是单位面积的辐射通量（面必须和光线垂直，否则要变成和投影面垂直的）。
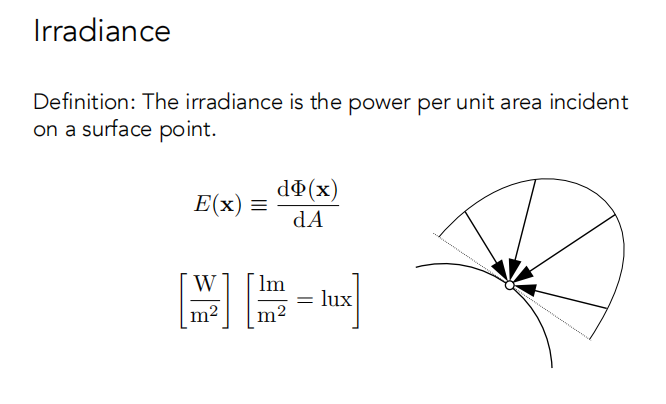
Irradiance 例子：
- 冬夏温度之分是因为点光源辐射的能量到达辐射点的角度不同步（阳光和不同区域的夹角不同），导致接收的能量不同。
- Irradiance 会衰减（不是 Intensity 衰减）
1.4.3 Radiance
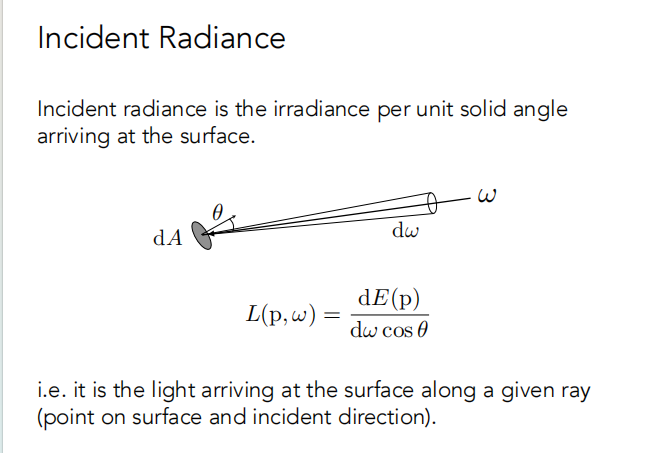
Radiance 描述光线在传播过程中的属性。
定义：
- 单位面积，单位立体角接受的能力；
- 或者理解为：在单位面积，单位立体角 发出的能量；
注意：
因为 Irradiance 是单位面积的辐射通量，Intensity 是单位立体角发出的能量。
所以 Radiance是每单位立体角的 Irradiance，Radiance是每单位面积的正交 Intensity。
1.4.3.1 Incident Radiance
Incident Radiance 是每单位立体角的到达表面的 Irradiance。
1.4.3.2 Exiting Radiance
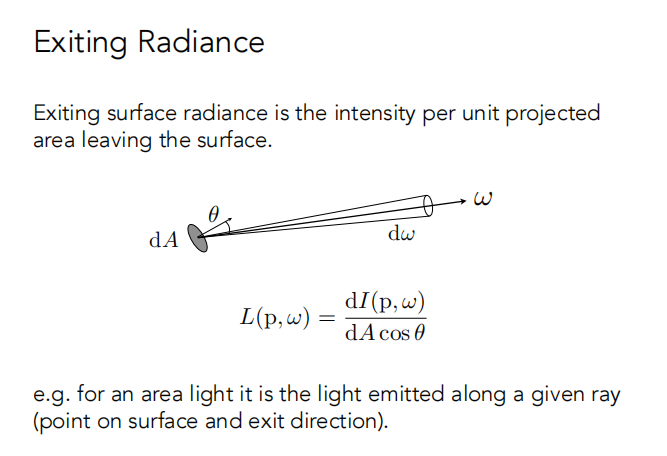
Exiting surface radiance 是每单位面积向某个角度辐射出的 Intensity（这里参考文章里面应该是写错了）。
1.5 Irradiance 和 Radiance
Irradiance：被区域 dA 吸收的所有的能量。
Radiance：被区域 dA 的来自d ω 的能量（多了一个立体角）。
1.6 各向同性点光源 Isotropic Point Source
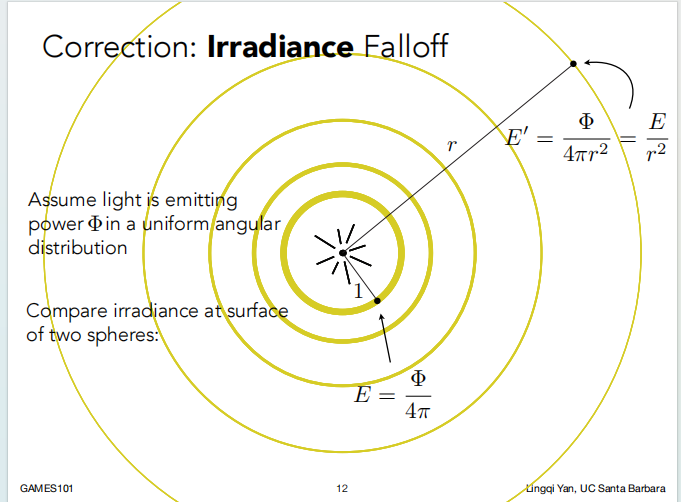
如果点光源均匀的辐射出光，则可以得到点光源的强度 I 如下所示。
2. 双向反射分布函数 Bidirectional Reflectance Distribution Function（BRDF）
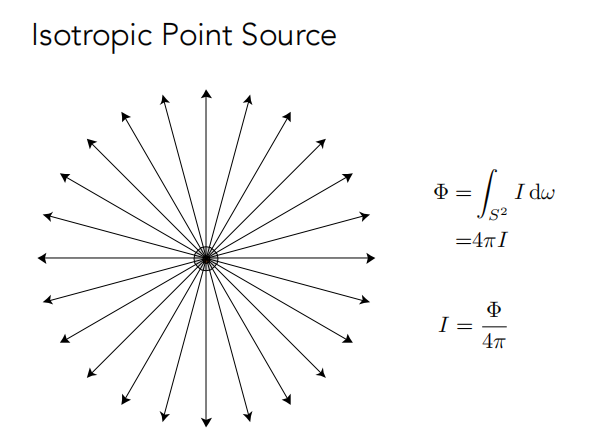
引入 ：
- 来自于 ωi 立体角的 Radiance 转化成 dA 接受的能量E，然后能量E会变成向着任何其他方向 ω 的 Radiance。
意义：
- BRDF 用于表示某个微小面积 dA 从某个微小立体角 dωi 接受的 Irradiance 会如何被分配到不同的立体角去。
定义：
如下图所示，从来自 ωi 立体角的 Irradiance（dE(ωi))，经过单位面积吸收后，向某一立体角 ωr 发射出去，发射出去的 Radiance 是 dLr(x , ωr)
BRDF 用于表示从每个入射方向进来的光线会每个向出射方向 ωr 反射的能量多少。
BRDF 就是任何一个出射方向的 Radiance 的微分 除以 在入射点上 Irradiance的微分，BRDF 如下所示。
2.1 反射方程（The Reflection Equation）
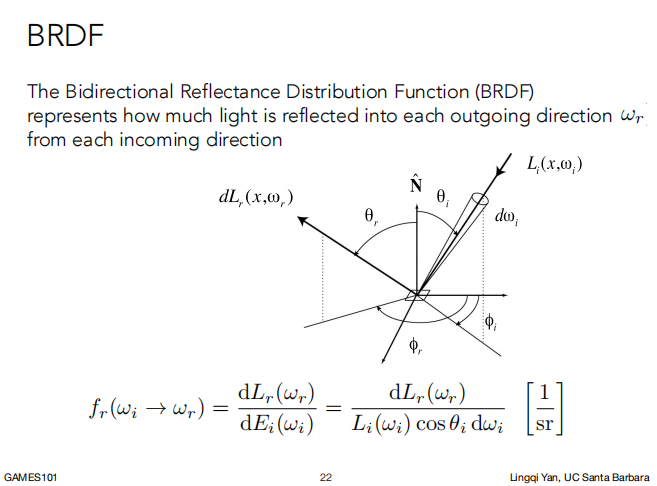
BRDF 是描述光线对物体时如何作用的，所以可以用于定义不同的材质。
把每一个方向对出射方向的贡献积分起来就会获得向某个方向反射出光照的结果。
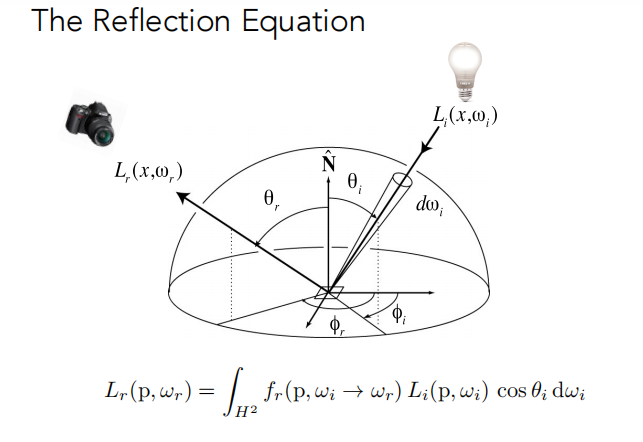
反射radiance取决于入射radiance，而入射Radiance不仅取决于光源，还有被其他物体反射的光，具有递归关系。
2.2 渲染方程（The Rendering Equation）
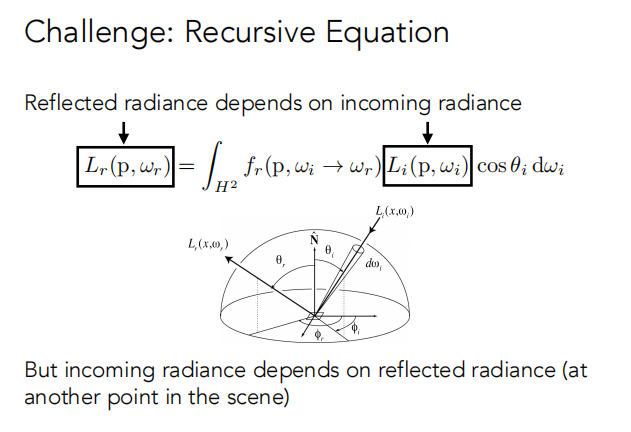
渲染方程 = 加上自己辐射的 Radiance + 反射方程
注意：
这里默认所有的方向 ω 都是向外的。
而且此时考虑的照亮到这一点的都是光源
但是实际上照亮这一点的不仅仅有光源的 Radiance，还有可能是其他物体反射过来的 Radiance；
如果考虑其他物体反射的radiance，就把反射物体和反射面当成光源，可以把渲染方程写成更通用的形式。
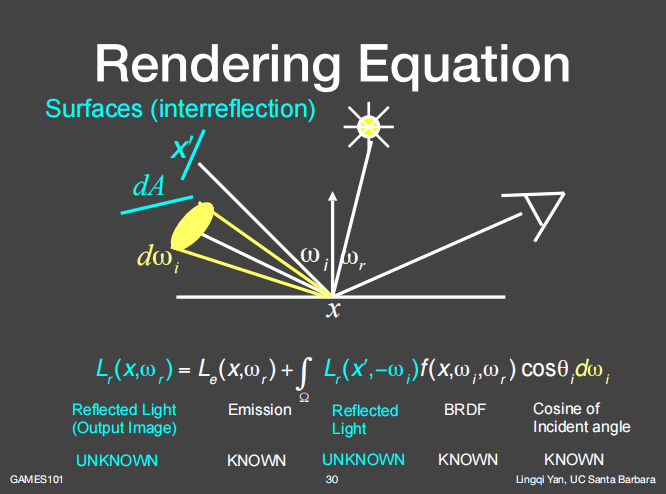
以上的式子可以简单的表达为：
K为反射操作符，进一步简写为：
可以看出L是递归定义的。
2.2.1 结论
简写渲染方程（L= E + K L）的目的是解出 L。
解L的方法如下所示，其中K也可以理解成反射次数，反射次数越多，项越多，K^2 代表光弹射两次。
全局光照 = 直接光照（E） + 间接光照（KE + K^2E + K^3E + …）
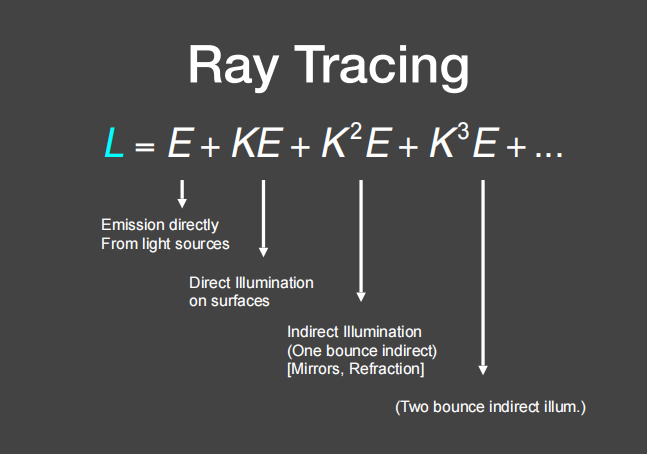
光栅化的着色一般只有 E+EK，而后面的间接光照部分光栅化难以做到，一般使用光线追踪（路径追踪）来进行计算。
参考：
好难…
光做笔记都要写好久好久…
【Games 101】Lec 16：光线追踪 4（蒙特卡罗积分，路径追踪）
Lecture 16：Ray Tracing 4 (Monte Carlo Path Tracing)
上一节课最后还讲了一点概率论，比较简单；
介绍了一个概念，后面常用，概率分布（密度）函数：
1. 蒙特卡洛积分（Monte Carlo Integration）
1.1 Why？
蒙特卡洛（Monte Carlo）积分目的是 解决定积分，但是它难以积分（解析式不好表达，不定积分不好求）的情况。
1.2 具体方法
1.2.1 基本思想
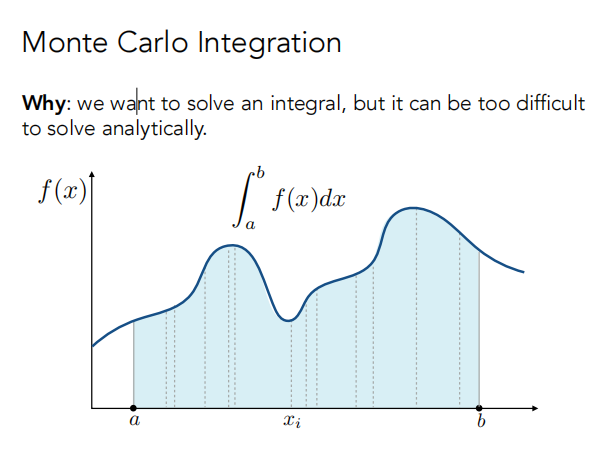
在积分域内不断采样，获得 y 值，不断的与 ab 范围获得一个个长方形，然后把所有长方形的面积相加求平均。
1.2.2 过程
在积分域 [a,b] 之间不断随机取样 xi，得到结果为 f(xi)，作为长方形的高，那么我们就能得到这次采样的长方形的面积 (b-a)*f(xi)（但是并不准确），当我们多次采样后求平均，那么他就准确了。
然后，采样的话可以用不同的概率密度函数p(x)；
对于给定函数 f(x) 的定积分，定义蒙特卡洛（Monte Carlo）积分：
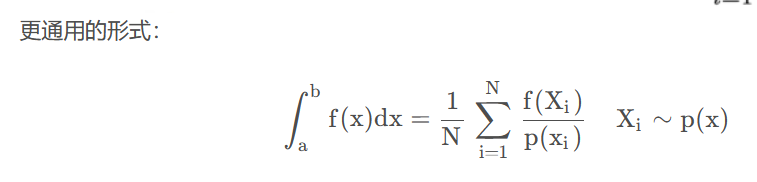
（其实不是很懂为什么这个 p(xi) 被放在了分母）
注意：
- N越大，得到的结果越精确。
- 在x上积分就一定要在x上取样。
1.2.3 例子
假如有一个均匀分布的概率分布函数，则他的蒙特卡洛积分为：
2. 路径追踪
2.1 动机：改进 Whitted-Style Ray Tracing
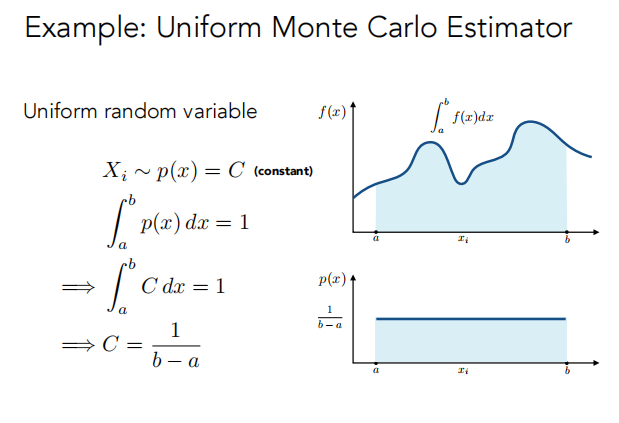
Whitted-Style Ray Tracing 对光线进行了如下假设：
- 总是进行镜面反射和折射
- 光线在漫反射面停止跳跃
2.1.1 Whitted-Style Ray Tracing 存在的问题
问题1：
- 如下是 Mirror reflection 和 Glossy reflection，但是对于打到Glossy的物体上的光线，传播的路径不能与Specular完全相同。
问题2：
- 对于漫反射物体，如果光线传播到它的表面上，那么还是会有光线传播的，不应该停止。
color bleeding：面的颜色流到其他的面上去。 就像上方右图高长方体的左面被全局光照映照出红色。
2.1.2 Whitted-Style Ray Tracing问题的解决办法
Whitted-Style Ray Tracing 是错的，但是渲染方程是正确的。
但是此方程涉及
- 解半球的积分
- 解决方法：使用Monte Carlo积分解渲染方程的积分。
- 递归
- 解决方法：使用俄罗斯轮盘法来结束递归。
2.2 使用Monte Carlo积分解渲染方程的积分
2.2.1 步骤
目的：渲染下面场景的一像素的直接光照。
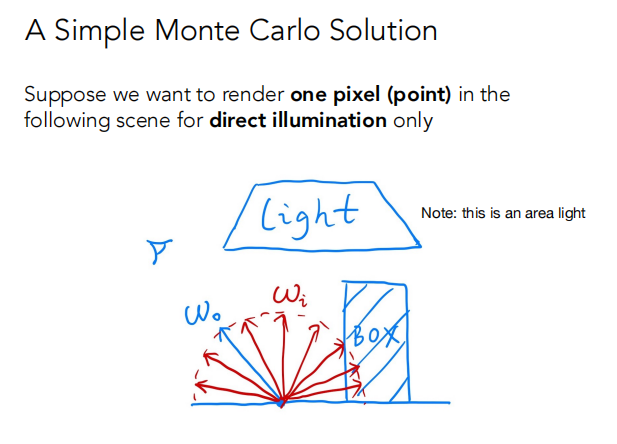
ω0：观测方向，从着色点到观测方向。
ωi：各个不同的入射的方向。
这里直接搬了参考文章中的分析：
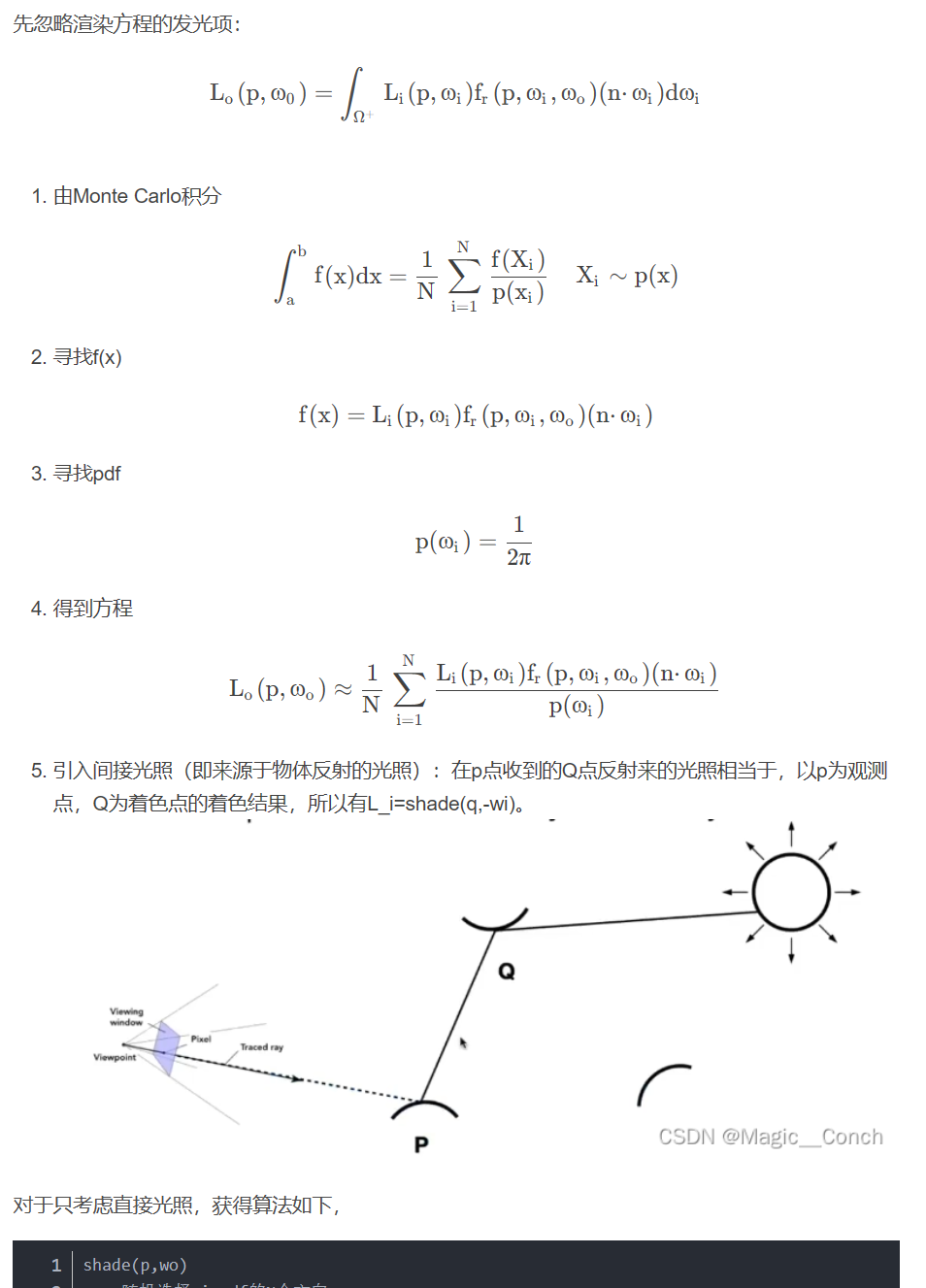
对于只考虑直接光照，算法如下：
1 | shade(p, wo) |
2.2.2 问题：路径追踪解决光线数量爆炸
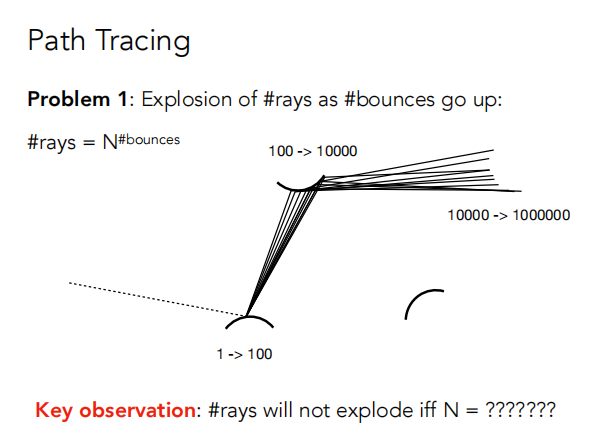
使用上面的方法，由于光线跳跃多次，光线的数量会爆炸（有递归）rays = N^bounces ;
解决方法 令N = 1，即每次只选取 wi~pdf 的一个方向。
路径追踪就是上面N=1的算法 ，即每次路径追踪只是随机选择一个方向反射。
1 | shade(p,wo) |
但是噪声会很大。但是只要对每个像素trace more paths并求它们radiance的平均就可以减少噪声。如下所示。
2.2.3 Ray Generation
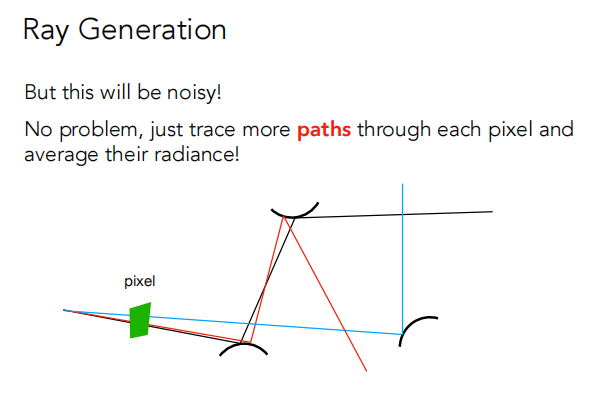
为了减少噪声，所以每个像素要生成多个光线，进行多次路径追踪，光线生成算法如下。
1 | ray_generation(camPos,pixel) |
其实这里也有点像蒙特卡洛积分，也是取平均；
2.3 使用俄罗斯轮盘（RR）解决递归算法停不下来
问题：
- 虽然现实中的光源跳跃也不会停，但是不停的话递归就无法结束。
解决方案：
- Russion Roulette(RR) 俄罗斯轮盘赌。
2.3.1 RR方法概述
设定一个概率，0<P<1。
- 有概率P，射出光线并且返回着色结果 Lo / P；
- 有概率1-P不射出光线，并返回结果0；
用这种方法，仍然可以期望得到值 Lo：
E = P ∗ (Lo / P) + (1 − P) ∗ 0 = Lo
2.3.2 RR方法改进后的路径追踪算法
进行如上改进后，得到的代码如下：
1 | shade(p,wo) |
这样就能保证递归可以停止。
2.4 提高 Path Tracing 的效率
问题 经过以上改进，现在路径追踪算法是正确的了，但是它不高效。
如下图所示，如果均匀的四面八方采样，对于很多光线只有极少数打到光源，大部分都被浪费掉了。
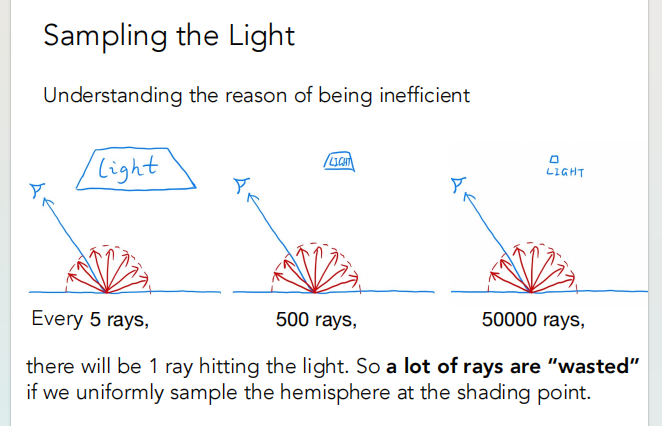
所以我们直接在光源上采样，pdf = 1/A，但是渲染方程的积分是在立体角上进行的；
由于Monte Carlo方程要求在哪里积分就在哪里取样，所以只要把 dω 转变成对 dA 积分即可。
我们得到立体角和光源面积微分 dA 的关系如下：
然后重写渲染方程：
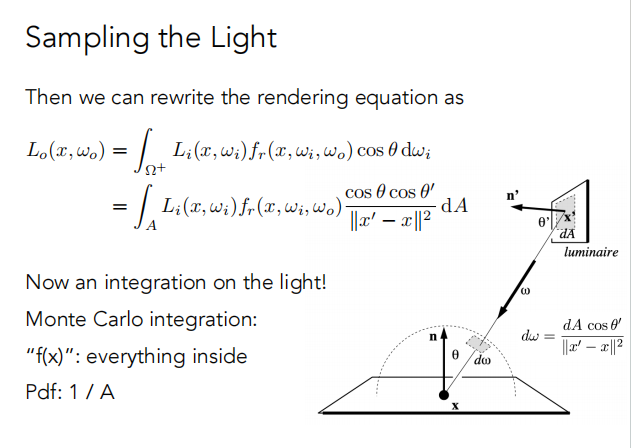
现在我们认为着色结果来源于两部分：
光源的贡献（直接采样光源，无需RR）
其他反射（indirect，需要RR）
伪代码如下：
再考虑另一个问题，如果光源和着色点之间被物体遮挡，则直接返回0。
到此 Path Tracing 算法完成。
2.5 Path Tracing的特点
缺点：路径追踪不好处理点光源。
优点：Path Tracing 可以做到照片级真实感PHOTO-REALISTIC（如下所示）。
3 Raytracing的概念区分
早期：
- Ray tracing == Whitted-style ray tracing
现代：
- 包含所有光线传播方法的集合
- （单向/双向）path tracing
- 光子映射 Photon mapping
- Metropoils light transport
- VCM / UPBR
参考：
太难啦
【Games 101】Lec 14：光线追踪 2（加速光线追踪 和 辐射度量学）
Lecture 14：Ray Tracing 2 (Acceleration & Radiometry)
概述
这节课讲了 光线追踪的加速 和 辐射度量学；
这篇文章写的是光线追踪的加速，辐射度量学一起放在下一篇文章；
上篇文章讲了包围盒，这节课前面讲的是如何用包围盒加速光线追踪；
均匀空间划分 Uniform Spatial Partitions （Grids）
预处理 – 建立加速格子
- 找到包围盒
- 创建格子
- 标记出和物体相交的格子
光线与场景求交点
- 依次遍历光线穿过的格子
- 如果这个格子被标记，则说明这个格子里面有物体，那么就计算光线是否和这个格子里面的物体相交
均匀空间划分的结果
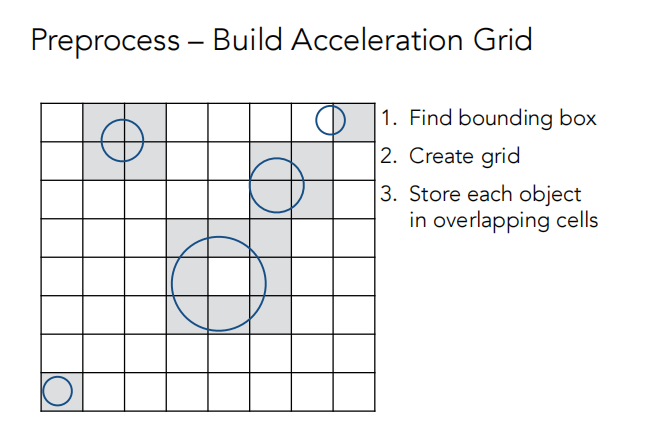
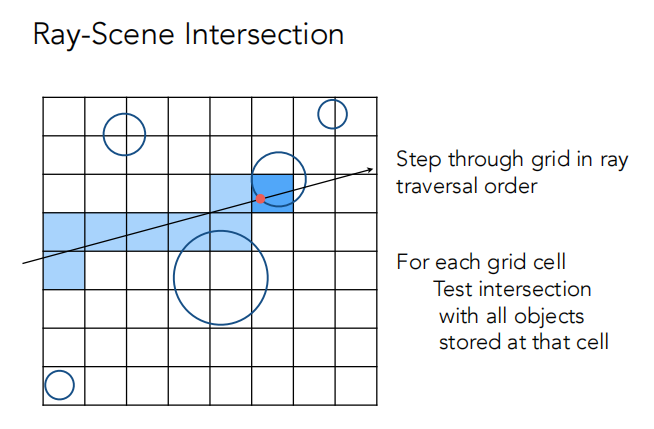
格子太多和格子太少都是不好的。
- 只有一个格子：没有加速效果。
- 格子特别密集：需要做很多光线与格子求交，加大开销。
- 下面是划分方式的经验之谈：
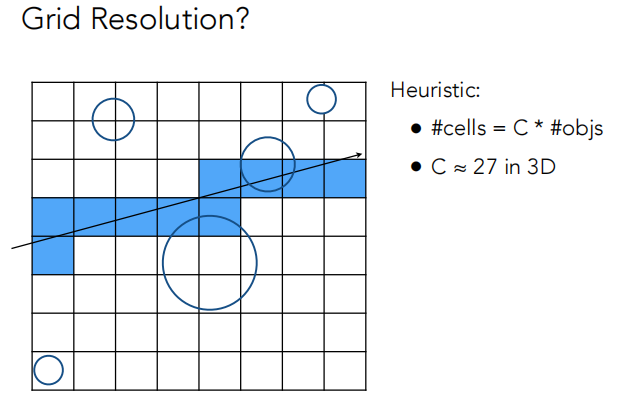
格子划分法适用于大小和空间均匀分布的大型对象集合（如下图所示）。
但是此方法不适合于有很多空旷区域的场景（如下图所示），下面又称为 “teapot in stadium” 问题。（其实就是分布不均的场景，有的地方物体很密，有的地方物体很稀疏）
空间划分（Spatial Partitions）
空间划分的方式
- Oct-Tree 八叉树 把场景包起来，然后把正方体切成八份（三维的就是8份，xyz各切一刀，但是上面的图是4份，因为是2维的，所以看起来是2^2）。不断的对子节点递归进行此过程，放格子里面是空的或者物体足够少就停下来。（但是有个严重的问题，随着维度的升高，节点数量指数型增长）
- KD-Tree 与八叉树几乎相同，但是对每次划分的格子，总是沿着某一个轴切割（通常是交替的），且对每个格子仅切割一次。（好处是相比于八叉树，节点数量的复杂度不会随着维度指数型增长。）（而且不用等分，看下面的例子好理解）
- BSP-Tree 对空间二分，每次划分时选择一个方向，与KD-Tree的区别在于它的切割不一定是与轴平行的。（存在的问题是在维度高的时候不好计算，切割的几何体从点到线到面到超平面。）
KD-Tree
KD-Tree 的基本结构
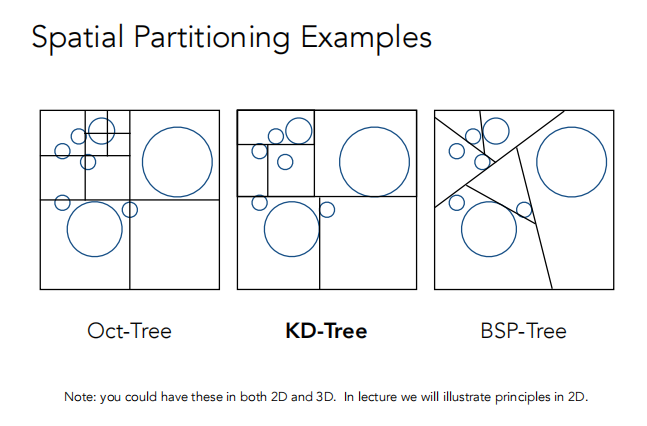
本质上是一颗二叉树，如下图所示（为了简化没画全，实际上1、2等节点都有子节点）。
- 对于非叶子节点
- 划分的轴：x、y或z轴。
- 划分的位置：分割的平面沿轴的坐标。
- 子节点：一定有两个子节点。
- 在非叶子节点不会存储物体。
- 对于叶子节点
- 存储物体列表。
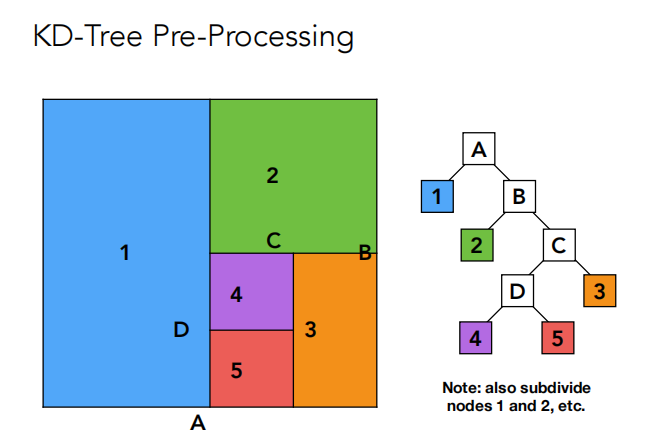
还是有点抽象？没事，看一下下面的应用：（最好看一下原视频）
计算光线与物体交点的步骤
- 如果走到非叶子节点，则探一下它的两个子节点（递归）
- 如果走到叶子节点，则：
- 如果包围盒里面没有物体，则跳过就行了；
- 如果有物体，则判断光线是否和物体相交；
KD-Tree的问题
- 很难判断物体的三角形和AABB包围盒是否有交集。（比如一个包围盒很小，整个嵌在了三角形的面里面，这个要怎么判断？）
- 一个物体可能会与很多AABB包围盒有交集。也即一个物体可能存储在多个叶子节点里。（计算起来比较废）
物体划分与BVH加速结构（Object Partition & Bounding Volume Hierarchy）
换一种思想，既然对空间划分这么麻烦，那么就直接划分物体；
思想和步骤
- 首先找到一个包围盒（这个简单啊，所有三角形坐标求min，max就行）
- 递归的把物体集合划分成两个子集；
- 重新计算子集的包围盒；
- 当满足一定要求的时候停止（比如规定一个包围盒里面只有五个三角形的时候）；
- 在每个叶子节点里存储所有物体；
下面是图解：
BVH 优点和缺点
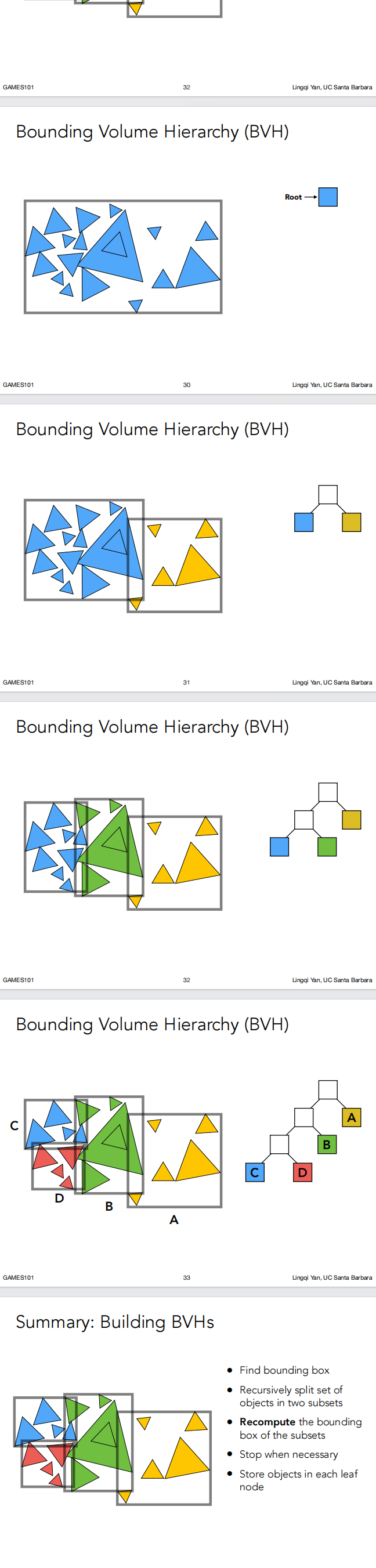
BVH避免了KD-Tree的问题，具有如下优点。
- 一个物体只能出现在一个格子里。
- 不涉及三角形和包围盒求交的问题。
缺点：
- BVH并没有把空间严格的划分开（包围盒有可能相交）。
BVH 的细节问题
如何划分节点？
每次都需要选择一个维度来分割（经验上有下面两种做法）。
- 选择节点中最长的轴。
- 取中间的物体的位置来划分节点。
如何存储 BVH 树？
- 中间节点存储包围盒和子节点的指针。
- 叶子节点存储包围盒和物体列表。
- 节点代表场景中图元（primitives）的子集，所有物体都在子树中。
伪代码
1 | -- 参考的是课件里面的 |
空间划分和物体划分
空间划分（如KD-tree）
- 把空间划分成不重叠的区域。
- 一个物体可能被包含在多个区域中。
物体划分（如BVH）
- 把物体划分成不相交的子集。
- 每个子集的包围盒在空间上可能是重叠的。
参考
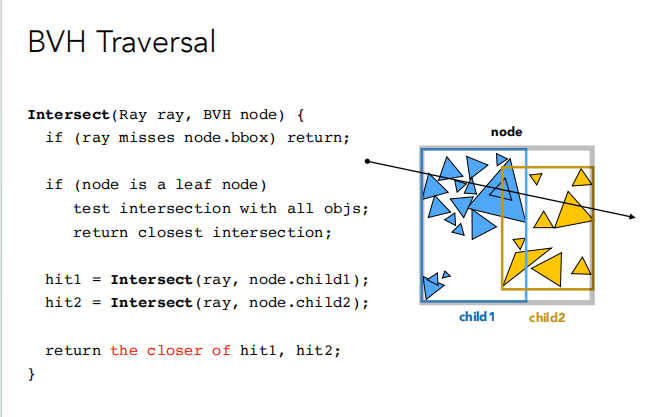
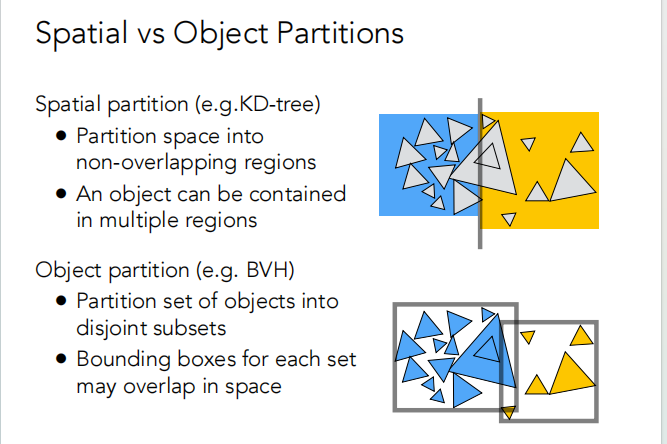
图形学笔记（十二）光线追踪2——使用AABB包围盒加速光线追踪、空间划分（八叉树、KD树、BSP树）、物体划分（BVH加速结构）、光线与物体求交_光线追踪算法遍历八叉树-CSDN博客
AI孙燕姿 真好听 hhh
等哪天闲了也来研究研究这东西。