Lecture 15:Ray Tracing 3 (Light Transport & Global Illumination)
这节课讲的是 Light Transport & Global Illumination 当然首先包含了上一节课最后的辐射度量学;
ps:这几节课是真的难…
1. 辐射度量学(Basic radiometry)
1.1 概述
辐射度量学的动机:
光源中定义L=10,但是10代表的是什么无法确定,缺少单位。
定义:
辐射度量学就是在物理上准确度量光照的方法。
它定义了一系列的方法和单位,准确的定义了光在空间中的属性:
- Radiant flux(辐射通量)
- intensity(辐射强度)
- irradiance(辐射[照]度)
- radiance(辐[射]亮度)
1.2 角,立体角(solid angle),微分立体角
- 角 Angle: 圆上的弧长与半径的比值。

- 立体角(solid angle):球面上的面积和半径平方的比值。(弧度制在三维空间的延申)

- 微分立体角(Differential)
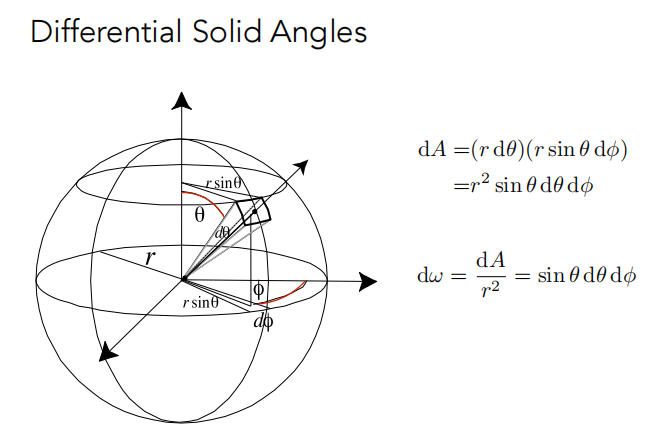
dA 是球面上的微分面积,近似成长方形
通过积分可以得到,整个球的立体角是 4π 。
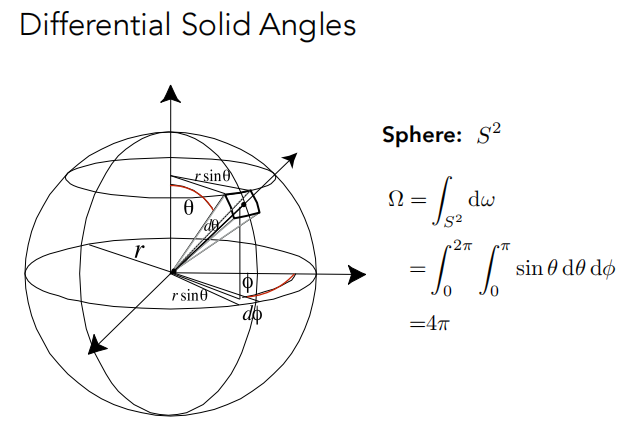
1.3 Radiant Energy and Flux (Power)
1.3.1 Radiant Energy
定义:Radiant energy是一种电磁辐射的能量。它由 焦耳(J=Joule)单位来度量,用符号Q来表示。
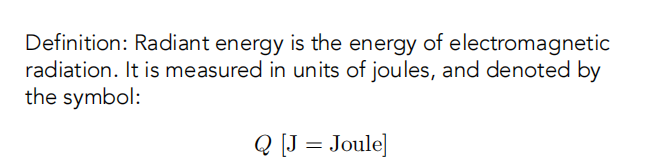
1.3.2 Radient Flux(Power)
定义:
- Radient flux(Power) 是单位时间的发射出的、反射的、传播的和接收的能量。
- 或者:单位时间辐射出光子的数量
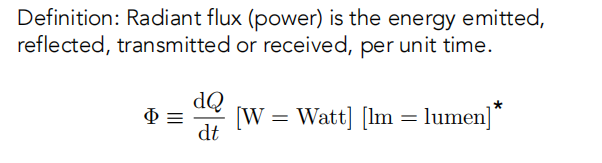
1.4 与光相关的物理量
主要是区别下面三种物理量:
- Radiant Intensity:光源辐射出的能量;
- Irrdiance:物体表面接收的光的能量;
- Radiance:光线在传播过程中的能量;
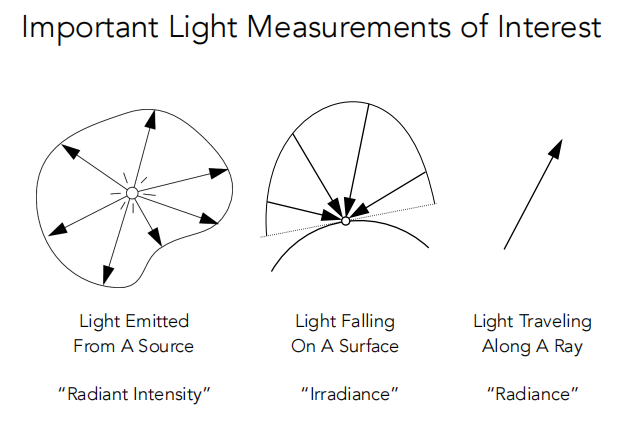
1.4.1 Radient intensity
定义:
- Radient intensity是 每单位立体角 辐射的能量。
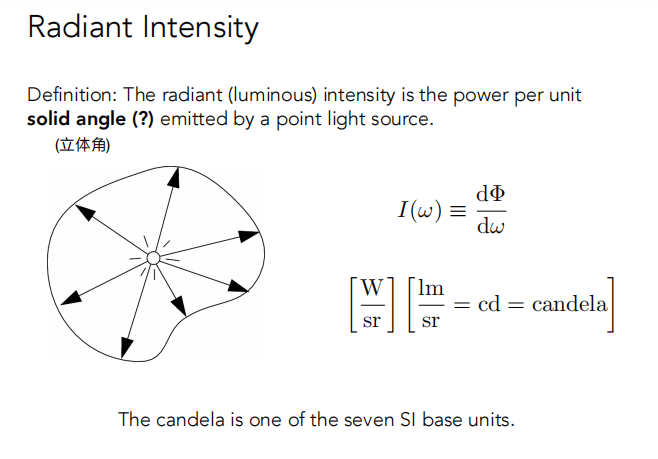
1.4.2 Irradiance
定义:
- Irradiance 是单位面积的辐射通量(面必须和光线垂直,否则要变成和投影面垂直的)。
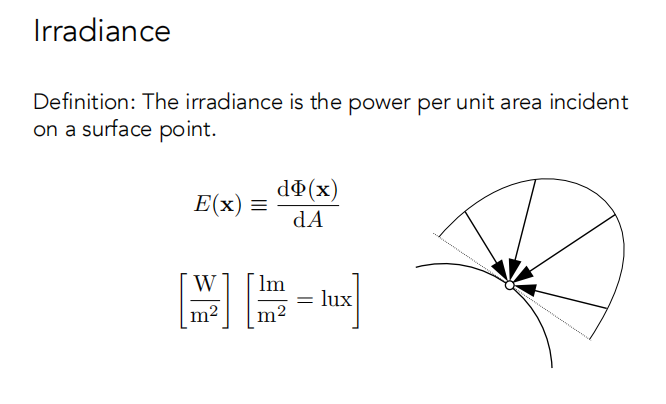
Irradiance 例子:
- 冬夏温度之分是因为点光源辐射的能量到达辐射点的角度不同步(阳光和不同区域的夹角不同),导致接收的能量不同。
- Irradiance 会衰减(不是 Intensity 衰减)
1.4.3 Radiance
Radiance 描述光线在传播过程中的属性。
定义:
- 单位面积,单位立体角接受的能力;
- 或者理解为:在单位面积,单位立体角 发出的能量;

注意:
因为 Irradiance 是单位面积的辐射通量,Intensity 是单位立体角发出的能量。
所以 Radiance是每单位立体角的 Irradiance,Radiance是每单位面积的正交 Intensity。
1.4.3.1 Incident Radiance
Incident Radiance 是每单位立体角的到达表面的 Irradiance。
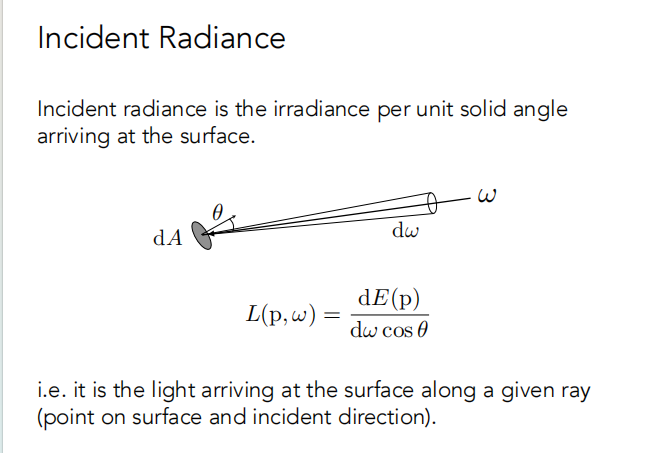
1.4.3.2 Exiting Radiance
Exiting surface radiance 是每单位面积向某个角度辐射出的 Intensity(这里参考文章里面应该是写错了)。
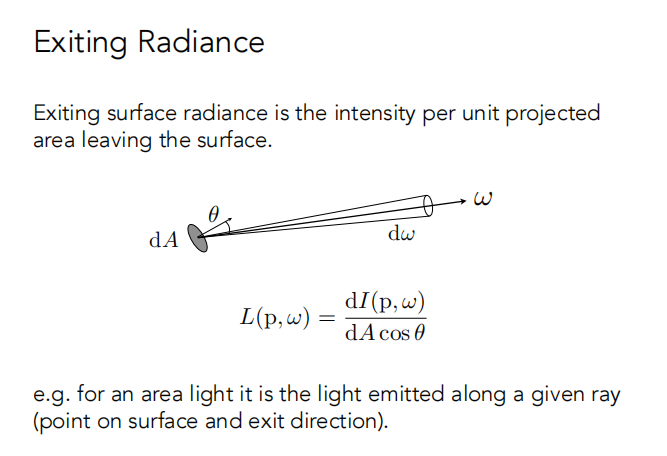
1.5 Irradiance 和 Radiance
Irradiance:被区域 dA 吸收的所有的能量。
Radiance:被区域 dA 的来自d ω 的能量(多了一个立体角)。

1.6 各向同性点光源 Isotropic Point Source
如果点光源均匀的辐射出光,则可以得到点光源的强度 I 如下所示。
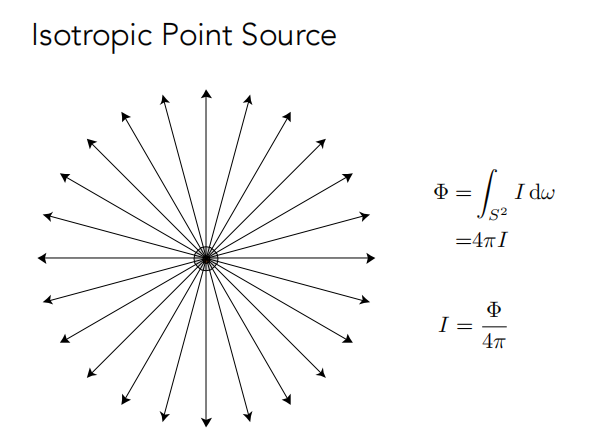
2. 双向反射分布函数 Bidirectional Reflectance Distribution Function(BRDF)
引入 :
- 来自于 ωi 立体角的 Radiance 转化成 dA 接受的能量E,然后能量E会变成向着任何其他方向 ω 的 Radiance。
意义:
- BRDF 用于表示某个微小面积 dA 从某个微小立体角 dωi 接受的 Irradiance 会如何被分配到不同的立体角去。
定义:
如下图所示,从来自 ωi 立体角的 Irradiance(dE(ωi)),经过单位面积吸收后,向某一立体角 ωr 发射出去,发射出去的 Radiance 是 dLr(x , ωr)

BRDF 用于表示从每个入射方向进来的光线会每个向出射方向 ωr 反射的能量多少。
BRDF 就是任何一个出射方向的 Radiance 的微分 除以 在入射点上 Irradiance的微分,BRDF 如下所示。
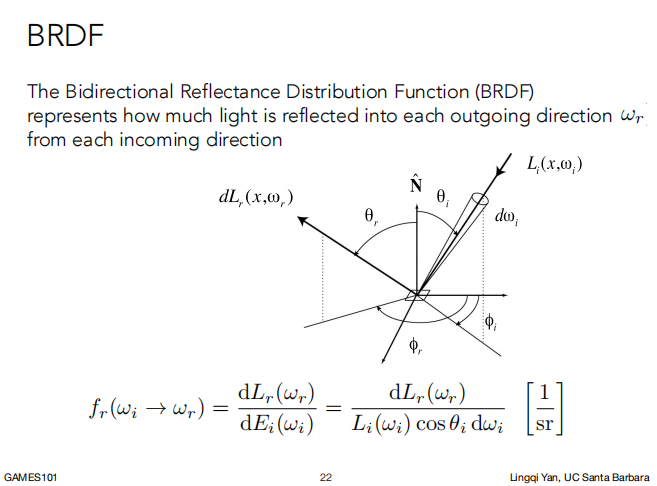
2.1 反射方程(The Reflection Equation)
BRDF 是描述光线对物体时如何作用的,所以可以用于定义不同的材质。
把每一个方向对出射方向的贡献积分起来就会获得向某个方向反射出光照的结果。
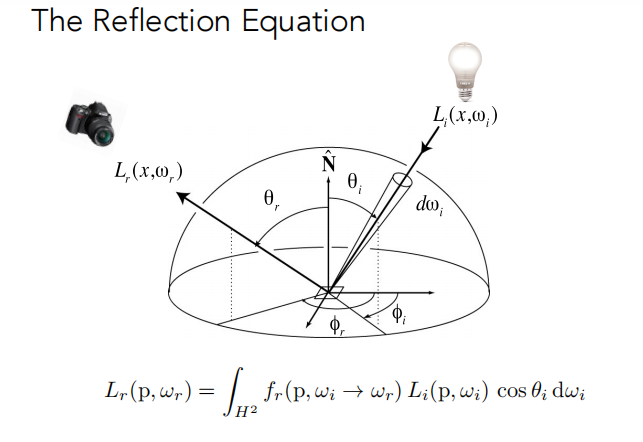
反射radiance取决于入射radiance,而入射Radiance不仅取决于光源,还有被其他物体反射的光,具有递归关系。
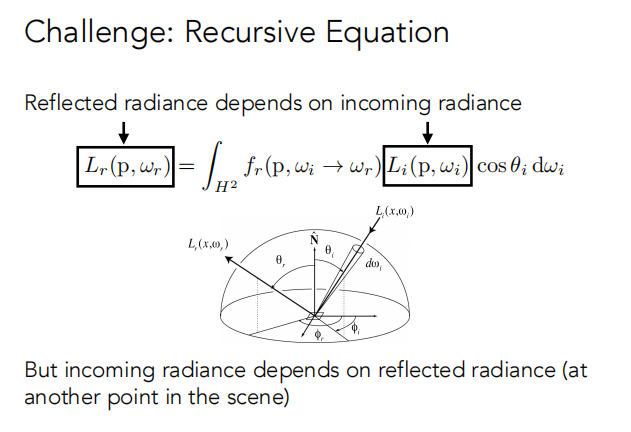
2.2 渲染方程(The Rendering Equation)
渲染方程 = 加上自己辐射的 Radiance + 反射方程

注意:
这里默认所有的方向 ω 都是向外的。
而且此时考虑的照亮到这一点的都是光源
但是实际上照亮这一点的不仅仅有光源的 Radiance,还有可能是其他物体反射过来的 Radiance;
如果考虑其他物体反射的radiance,就把反射物体和反射面当成光源,可以把渲染方程写成更通用的形式。
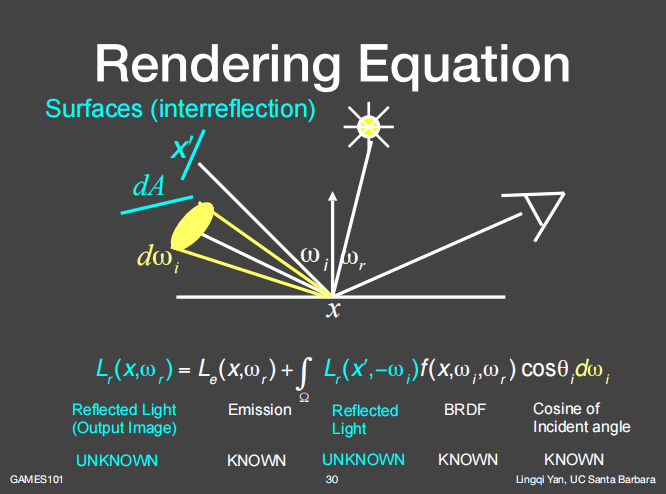
以上的式子可以简单的表达为:

K为反射操作符,进一步简写为:

可以看出L是递归定义的。
2.2.1 结论
简写渲染方程(L= E + K L)的目的是解出 L。
解L的方法如下所示,其中K也可以理解成反射次数,反射次数越多,项越多,K^2 代表光弹射两次。

全局光照 = 直接光照(E) + 间接光照(KE + K^2E + K^3E + …)
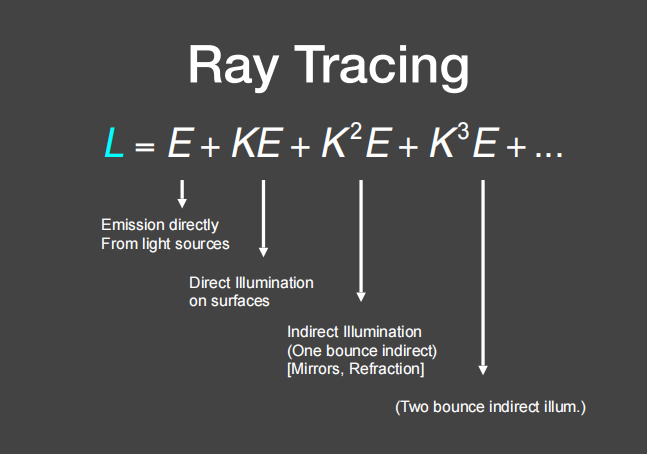
光栅化的着色一般只有 E+EK,而后面的间接光照部分光栅化难以做到,一般使用光线追踪(路径追踪)来进行计算。
参考:
好难…
光做笔记都要写好久好久…