FJBQ
0%

【Games 101】Lec 16：光线追踪 4（蒙特卡罗积分，路径追踪）

发表于 分类于 ，

Lecture 16：Ray Tracing 4 (Monte Carlo Path Tracing)

上一节课最后还讲了一点概率论，比较简单；

介绍了一个概念，后面常用，概率分布（密度）函数：

1. 蒙特卡洛积分（Monte Carlo Integration）

1.1 Why？

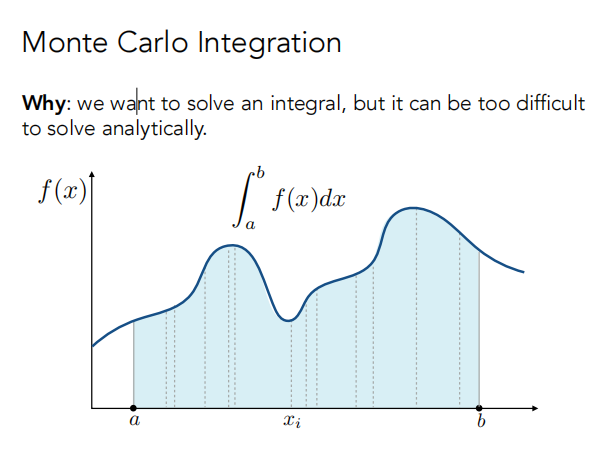
蒙特卡洛（Monte Carlo）积分目的是 解决定积分，但是它难以积分（解析式不好表达，不定积分不好求）的情况。

1.2 具体方法

1.2.1 基本思想

在积分域内不断采样，获得 y 值，不断的与 ab 范围获得一个个长方形，然后把所有长方形的面积相加求平均。

1.2.2 过程

在积分域 [a,b] 之间不断随机取样 xi，得到结果为 f(xi)，作为长方形的高，那么我们就能得到这次采样的长方形的面积 (b-a)*f(xi)（但是并不准确），当我们多次采样后求平均，那么他就准确了。

然后，采样的话可以用不同的概率密度函数p(x)；

对于给定函数 f(x) 的定积分，定义蒙特卡洛（Monte Carlo）积分：

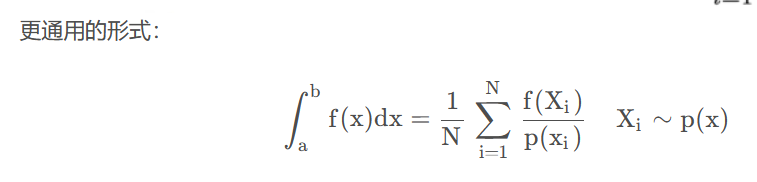
（其实不是很懂为什么这个 p(xi) 被放在了分母）

注意：

  • N越大，得到的结果越精确。
  • 在x上积分就一定要在x上取样。

1.2.3 例子

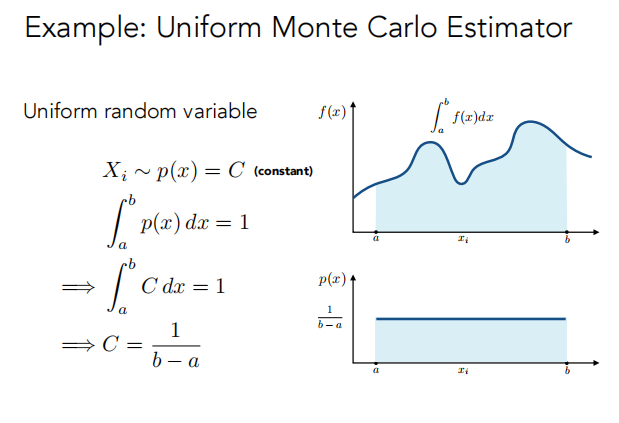
假如有一个均匀分布的概率分布函数，则他的蒙特卡洛积分为：

2. 路径追踪

2.1 动机：改进 Whitted-Style Ray Tracing

Whitted-Style Ray Tracing 对光线进行了如下假设：

  • 总是进行镜面反射和折射
  • 光线在漫反射面停止跳跃

2.1.1 Whitted-Style Ray Tracing 存在的问题

问题1：

  • 如下是 Mirror reflection 和 Glossy reflection，但是对于打到Glossy的物体上的光线，传播的路径不能与Specular完全相同。

问题2：

  • 对于漫反射物体，如果光线传播到它的表面上，那么还是会有光线传播的，不应该停止。

color bleeding：面的颜色流到其他的面上去。 就像上方右图高长方体的左面被全局光照映照出红色。

2.1.2 Whitted-Style Ray Tracing问题的解决办法

Whitted-Style Ray Tracing 是错的，但是渲染方程是正确的。

但是此方程涉及

  • 解半球的积分
    • 解决方法：使用Monte Carlo积分解渲染方程的积分。
  • 递归
    • 解决方法：使用俄罗斯轮盘法来结束递归。

2.2 使用Monte Carlo积分解渲染方程的积分

2.2.1 步骤

目的：渲染下面场景的一像素的直接光照。

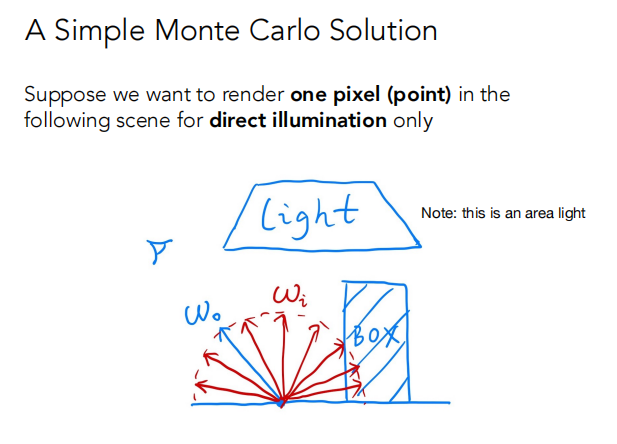
ω0：观测方向，从着色点到观测方向。

ωi：各个不同的入射的方向。

这里直接搬了参考文章中的分析：

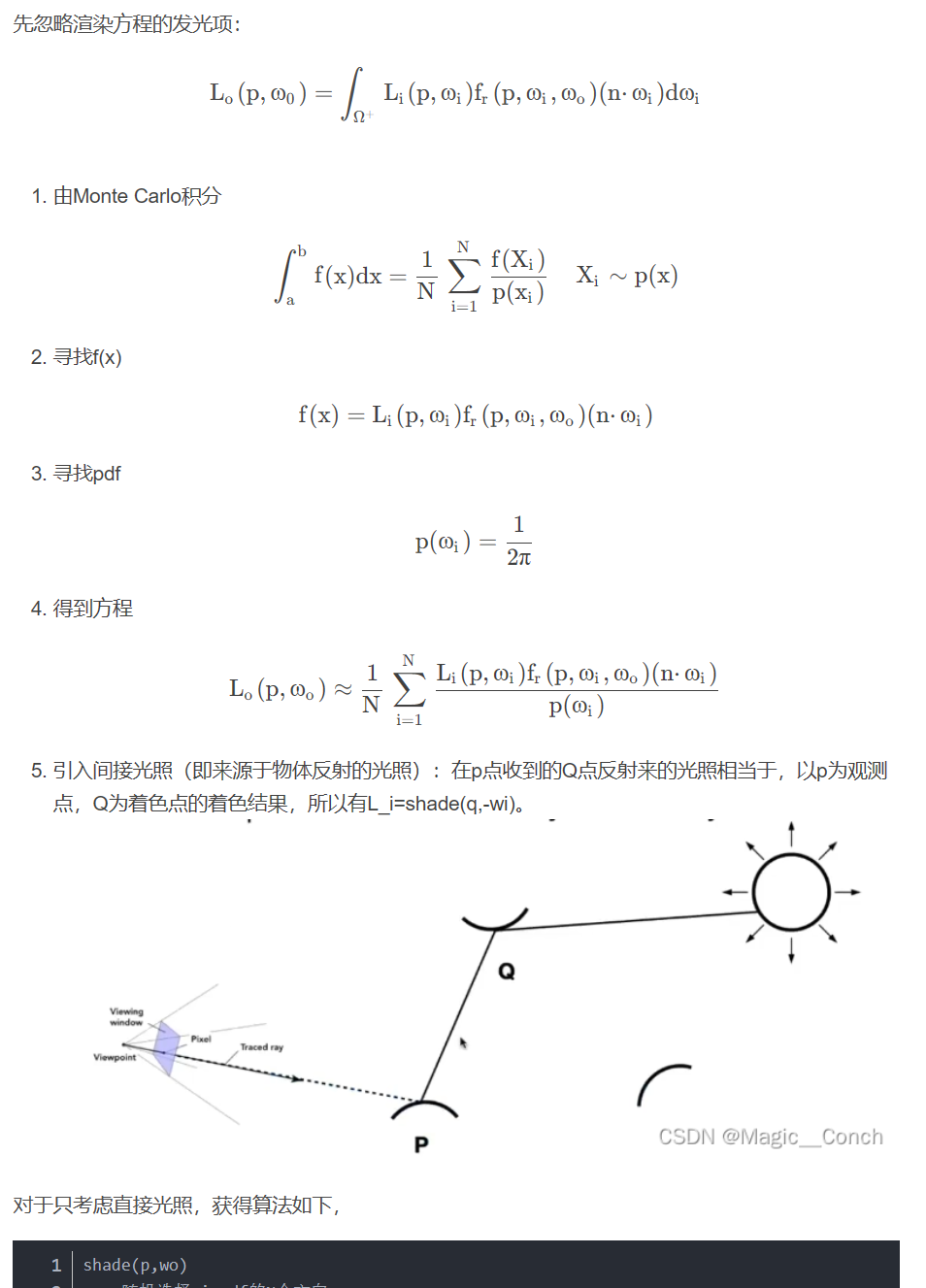
对于只考虑直接光照，算法如下：

1
2
3
4
5
6
7
8
9
10
shade(p, wo)
	随机选择 wi ~ pdf 的 N 个方向
	Lo=0.0
	for 每个 wi
		追踪一个光线r(p,wi)
		if 光线打到了光源
			Lo += (1/N) * L_i * f_r * cosine / pdf(wi)
		else if r达到了一个物体上的q点
			Lo += (1/N) * shade(q,-wi) * f_r * cosine / pdf(wi)			
	return Lo

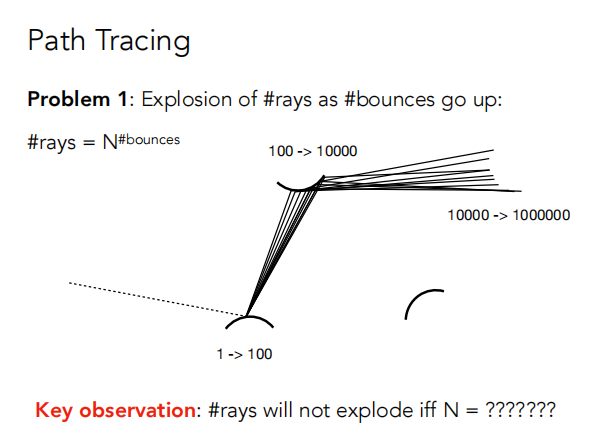
2.2.2 问题：路径追踪解决光线数量爆炸

使用上面的方法，由于光线跳跃多次，光线的数量会爆炸（有递归）rays = N^bounces ;

解决方法 令N = 1，即每次只选取 wi~pdf 的一个方向。

路径追踪就是上面N=1的算法 ，即每次路径追踪只是随机选择一个方向反射。

1
2
3
4
5
6
7
shade(p,wo)
	随机选择 wi~pdf 的1个方向
	追踪一个光线r(p,wi)
	if 光线r打到了光源
		return L_i * f_r * cosine / pdf(wi)
	else if r达到了一个物体上的q点
		return shade(q,-wi) * f_r * cosine / pdf(wi)

但是噪声会很大。但是只要对每个像素trace more paths并求它们radiance的平均就可以减少噪声。如下所示。

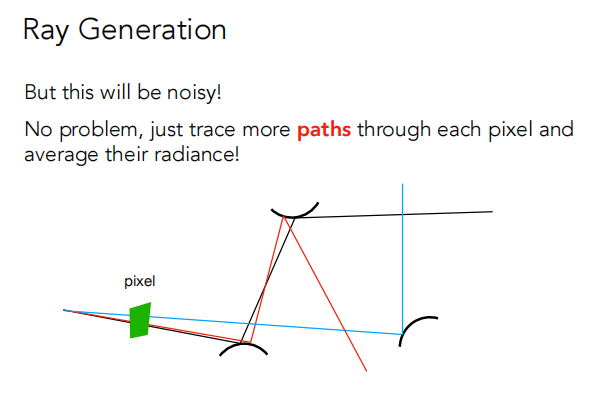
2.2.3 Ray Generation

为了减少噪声，所以每个像素要生成多个光线，进行多次路径追踪，光线生成算法如下。

1
2
3
4
5
6
7
8
ray_generation(camPos,pixel)
   在像素中平均的选取N个采样点
   pixel_radiance = 0.0
   for 对于像素中的每个采样点
   	射出一条光线r(camPos,cam_to_sample)
   	如果光线击中了场景中的p点
   		pixel_radiance += 1 / N * shade(p, sample_to_cam)
   return pixel_radiance

其实这里也有点像蒙特卡洛积分，也是取平均；

2.3 使用俄罗斯轮盘（RR）解决递归算法停不下来

问题：

  • 虽然现实中的光源跳跃也不会停，但是不停的话递归就无法结束。

解决方案：

  • Russion Roulette(RR) 俄罗斯轮盘赌。

2.3.1 RR方法概述

设定一个概率，0<P<1。

  • 有概率P，射出光线并且返回着色结果 Lo / P；
  • 有概率1-P不射出光线，并返回结果0；

用这种方法，仍然可以期望得到值 Lo：

E = P ∗ (Lo / P) + (1 − P) ∗ 0 = Lo

2.3.2 RR方法改进后的路径追踪算法

进行如上改进后，得到的代码如下：

1
2
3
4
5
6
7
8
9
10
11
shade(p,wo)
	手动指定一个概率 P_RR
	在均匀分布[0,1]范围内随机选择ksi。
	if(ksi > P_RR) return 0.0;

	随机选择 wi~pdf 的1个方向
	追踪一个光线r(p,wi)
	if 光线r打到了光源
		return L_i * f_r * cosine / pdf(wi) / P_RR
	else if 光线r达到了一个物体上的q点
		return shade(q,-wi) * f_r * cosine / pdf(wi) / P_RR

这样就能保证递归可以停止。

2.4 提高 Path Tracing 的效率

问题 经过以上改进，现在路径追踪算法是正确的了，但是它不高效。

如下图所示，如果均匀的四面八方采样，对于很多光线只有极少数打到光源，大部分都被浪费掉了。

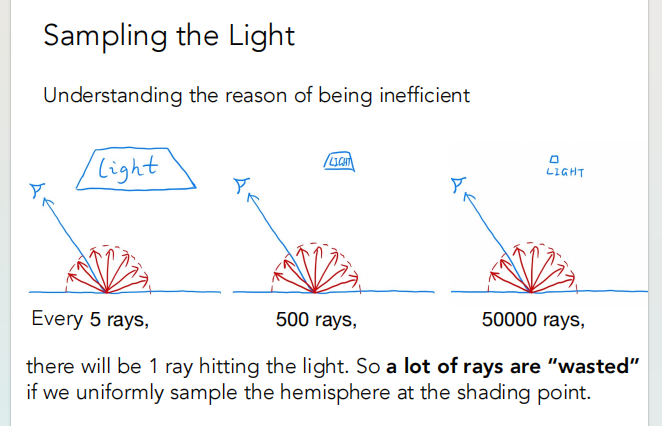
所以我们直接在光源上采样，pdf = 1/A，但是渲染方程的积分是在立体角上进行的；

由于Monte Carlo方程要求在哪里积分就在哪里取样，所以只要把 dω 转变成对 dA 积分即可。

我们得到立体角和光源面积微分 dA 的关系如下：

然后重写渲染方程：

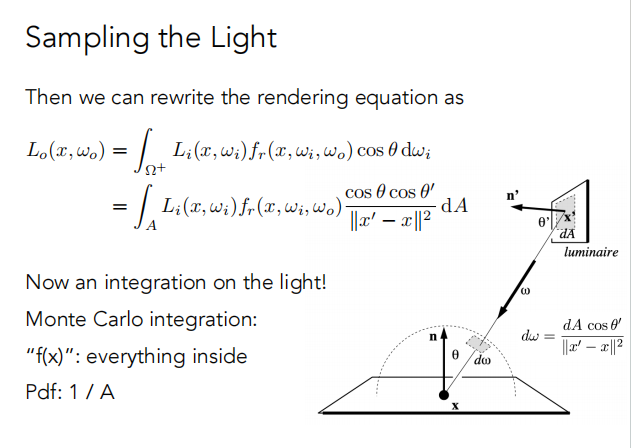
现在我们认为着色结果来源于两部分：

  • 光源的贡献（直接采样光源，无需RR）

  • 其他反射（indirect，需要RR）

伪代码如下：

再考虑另一个问题，如果光源和着色点之间被物体遮挡，则直接返回0。

到此 Path Tracing 算法完成。

2.5 Path Tracing的特点

缺点：路径追踪不好处理点光源。

优点：Path Tracing 可以做到照片级真实感PHOTO-REALISTIC（如下所示）。

3 Raytracing的概念区分

早期：

  • Ray tracing == Whitted-style ray tracing

现代：

  • 包含所有光线传播方法的集合
  • （单向/双向）path tracing
  • 光子映射 Photon mapping
  • Metropoils light transport
  • VCM / UPBR

参考：

图形学笔记（十四）光线追踪4——蒙特卡洛（Monte Carlo）积分、路径追踪详细过程（Whitted-Style的问题于RR（俄罗斯轮盘赌）算法、Ray Generation）、照片级真实感渲染_图形学rr-CSDN博客

太难啦

欢迎关注我的其它发布渠道