Lecture 22:Animation (cont.)
1 单个粒子模拟(Single Particle Simulation)
1.1 单个粒子的运动
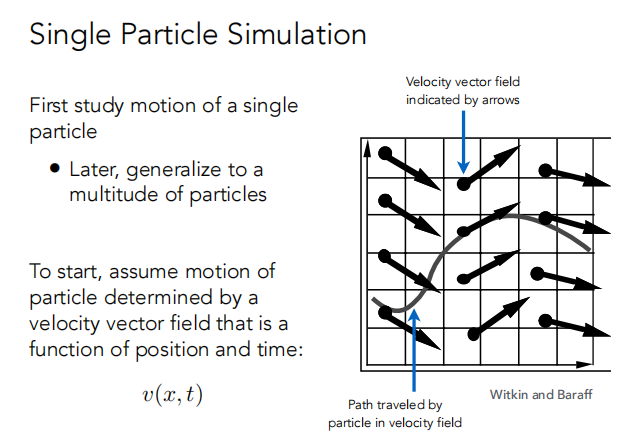
首先研究一个粒子的运动然后泛化到大多数粒子。
我们线认为粒子的运动由速度场(velocity vector field)决定,这个速度场就是一个位置和时间的函数:v(x,t)
知道粒子的位置和时间,就知道它的速度;(这个函数我们现在是已知的)
那么,计算粒子的位置(随时间变化)需要解一个一阶的常微分方程(不存在对其他变量的微分或导数First-order意味着只存在一阶导数):

1.2 欧拉方法(Euler’s Method)
1.2.1 概述
欧拉方法是一种简单的迭代方法,经常被使用、不准确、大多数都不稳定。
可以使用欧拉方法对给定初始位置和速度场的点求解经过时间t后所处的位置。

1.2.2 误差
使用数值计算的方法积分,误差会累计,最后的Euler积分结果会很差。

1.2.3 欧拉方法的不稳定性(Instability of the Euler Method)
如下图,粒子的轨迹始终不能沿着圆形或指定的轨迹。
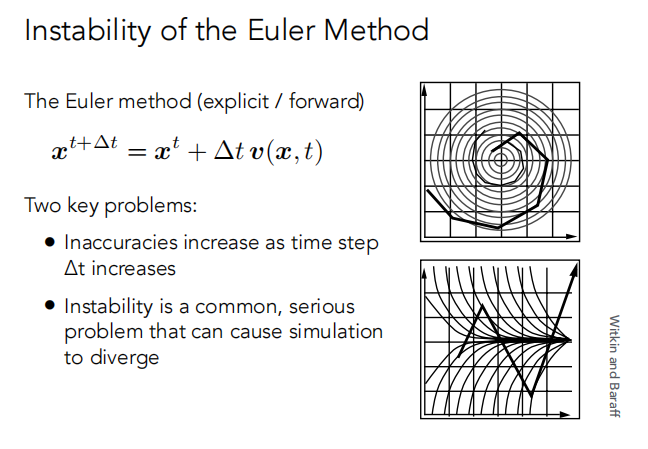
即欧拉方法有两个关键的问题:
- 误差随着时间步长 Δt 的增加而增加。
- 不稳定性是一个普遍且严重的问题,它能造成模拟 diverge。
1.2.4 Errors 和 Instability
用有限差分数值积分法求解
导致两个问题:
Errors:
- 每个时间步的误差累积。精度随着模拟的进行而降低
- 在图形应用中,准确性可能不是关键
Instability:
- 错误可以复合,导致模拟甚至发散当底层系统没有
- 缺乏稳定性是模拟中的一个基本问题不容忽视
1.3 克服不稳定性的方法
1.3.1 概述
- 中点法/修正欧拉法
- 起点和终点的平均速度
- 自适应步长
- 递归地比较一步和两个半步,直到可以接受错误
- 隐式方法
- 使用下一个时间步骤的速度(硬)
- 基于位置/ Verlet的集成
- 在时间步长后约束粒子的位置和速度
1.3.2 中点法(Midpoint Method)
- 使用欧拉方法计算,点到达A( a )。
- 使用欧拉方法计算上一步起始点与A点的导数( b )。
- 使用中点的导数来重新更新位置( c )。
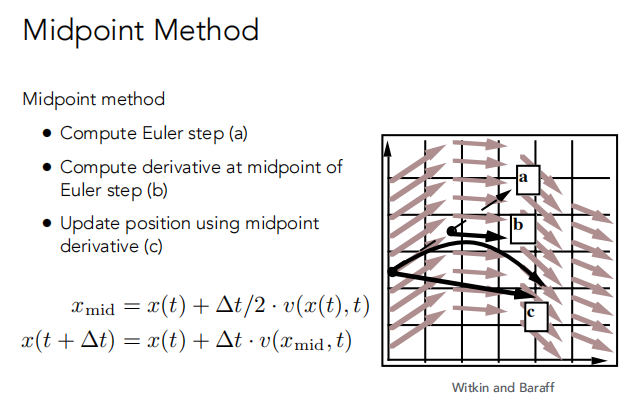
中点法比欧拉方法多了一个二次的项。

1.3.3 自适应步长法(Adaptive Step Size)
- 使用步长为T计算一个欧拉步骤来获得 X(T)
- 计算两个欧拉步骤,步长为T/2,获得 X(T/2)
- 计算error ∣∣ X(T) − X(T/2) ∣∣
- If ( error > threshold ) 减少步长并重复上面的步骤。
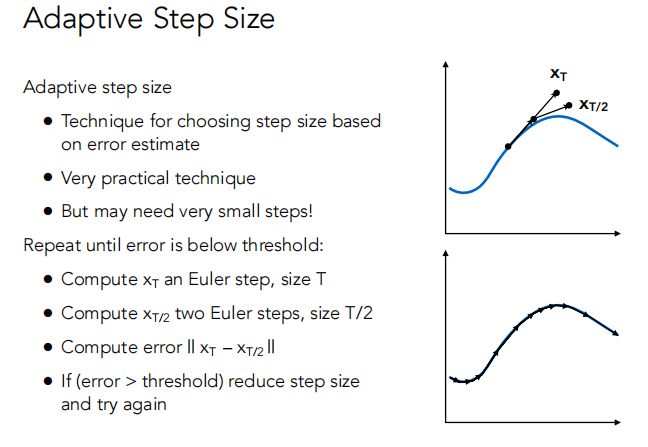
Adaptive 是基于 error 估计选择步长的方法,非常实用,但可能得到的步长会很小。
1.3.3 隐式欧拉方法
也被称作后向方法,使用下一时间的导数来计算当前的步骤。


定义与量化 “stability” (稳定性)的方法
- 使用局部截断误差(每个Δ \DeltaΔ的误差)/ 总截断累积误差(整体累加后的误差)来研究稳定性。
- 研究数的大小无意义,有意义的事研究它们的阶。
- 隐式欧拉方法的阶数为1,意味着局部截断误差为 O(h^2) 且全局阶段误差为 O(h)(h就是步长,定义为 Δt)。
- O(h)的理解:如果将 h 减半,预期误差也会减半。

1.3.4 Runge-Kutta Families
Runge-Kutta方法是一系列用于求解 ODE 的高级方法。
特点
- 擅长处理非线性问题。
- 它的四阶版是使用最广泛的,又名 RK4。

h就是步长,也就是 Δt
1.3.5 Position-Based / Verlet Integration
这是一种不基于物理的方法,通过调整物体的位置使物体满足某种性质。
思想:
- 在修改欧拉前步(forward-step)之后,约束粒子的位置以防止divergent、不稳定的现象。
- 使用约束位置计算速度。
- 这两种思想都会耗散能量,使其具有稳定性。
特点:
- 快速又简单。
- 不是基于物理模拟的,不满足能量守恒。
2 刚体模拟(Rigid Body Simulation)
刚体模拟与模拟单个粒子相似,只需额外考虑一些属性(角度,角速度)

3 流体模拟(Fluid Simulation)
3.1 基于位置的简单流体模拟方法
关键思想
- 认为水是由刚体小球组成的。
- 认为水是不可压缩的。
- 只要某处的密度海绵,就需要通过改变粒子的位置来“纠正”。
- 需要知道任何位置的密度的梯度。
- 使用梯度下降法来进行更新。

3.2 质点法和网络法(Eulerian vs. Lagrangian)

3.3 Material Point Method (MPM)
MPM 是一种混合的(Hybrid),结合 Eulerian 和 Lagrangian 的方法。
- Lagrangian:认为粒子带有材质属性。
- Eulerian:使用网格来做数值积分。
- lnteraction:粒子将属性传递给网格,网格执行更新,然后插值回粒子。

参考
结束,下面把作业做一做,然后打算做个玩具渲染器(当作毕设了…)