【Games 101】HomeWork 0：虚拟机的使用

HomeWork 0：虚拟机的使用

配环境…

真的是一波三折啊，捣鼓了好久…

还好虚拟机里面什么都有了

首先按照 pdf 里面的流程走就行了，下面记录一下一些问题：

黑屏…

我是重启之后就会黑屏，还没输入密码呢…

这个问题我直接删掉虚拟机，如何重新创建一个就好了；

安装 增强功能 显示 无法挂载光盘什么的

首先检查一下虚拟机是否有 VBox_GAs_… 光盘，有的话先弹出他，然后再尝试安装；

然后可能会失败，看下面这两篇：

VirtualBox 安装 ubuntu后安装增强工具无效的解决办法 - 知乎 (zhihu.com)

VirtualBox：unable to access “VBox_GAS_6.8.XXX-CSDN博客

成功安装之后就能：

调整虚拟机的分辨率；

主机和虚拟机之间拖拽文件；

等；

然后继续照着 pdf 里面操作就行了

代码

下面是作业0的代码：

#include<cmath>
#include<eigen3/Eigen/Core>
#include<eigen3/Eigen/Dense>
#include<iostream>
using namespace std;

void Test()
{
    // 这个一些基本运算
    std::cout << "Example of cpp \n";
    float a = 1.0, b = 2.0;
    std::cout << a << std::endl;
    std::cout << a/b << std::endl;
    std::cout << std::sqrt(b) << std::endl;
    std::cout << std::acos(-1) << std::endl;
    std::cout << std::sin(30.0/180.0*acos(-1)) << std::endl;

    // Example of vector
    std::cout << "Example of vector \n";
    //这个 Vector3f 是定义了一个三维向量，float(注意这里其实也就是一个 3x1 的矩阵)
    Eigen::Vector3f v(1.0f,2.0f,3.0f);
    Eigen::Vector3f w(1.0f,0.0f,0.0f);
    // vector output
    std::cout << "Example of output \n";
    std::cout << v << std::endl;
    // vector add
    std::cout << "Example of add \n";
    std::cout << v + w << std::endl;
    // vector scalar multiply
    std::cout << "Example of scalar multiply \n";
    std::cout << v * 3.0f << std::endl;
    std::cout << 2.0f * v << std::endl;

    // Example of matrix
    std::cout << "Example of matrix \n";
    /*
        这个 Matrix3f 是定义了一个3x3的float的矩阵；
        其实跳进去看源码就知道了，通过模板和宏定义实现的；
    */ 
    Eigen::Matrix3f i,j,ans;
    i << 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0;
    j << 2.0, 3.0, 1.0, 4.0, 6.0, 5.0, 9.0, 7.0, 8.0;
    // matrix output
    cout << "Example of output \n";
    cout << i << "\n\n";
    
    // matrix add i + j
    cout << "this is matrix add : \n";
    ans = i + j;
    cout << ans << "\n\n";

    // matrix scalar multiply i * 2.0
    cout << "this is matrix scalar multiply : \n";
    ans = i * 20;
    cout << ans << "\n\n";

    // matrix multiply i * j
    cout << "this is matrix multiply : \n";
    ans = i * j;
    cout << ans << "\n\n";

    /*
    matrix multiply vector i * v
    这个就是定义一个自定义大小的float矩阵，我这里定义的是 1x3 的；
    因为 v 是一个 1x3 的，i 是一个 3x3 的；
    */
    cout << "this is matrix multiply vector : \n";
    Eigen::MatrixXf ans1(1,3);
    ans1 = i * v;
    cout << ans1 << "\n\n";
}

/*
作业描述:
    给定一个点 P=(2,1), 将该点绕原点先逆时针旋转 45◦，再平移 (1,2), 计算出变换后点的坐标（要求用齐次坐标进行计算）。


分析：
    1. 首先说到要用齐次坐标表示，我们回顾一下，2维的点用齐次坐标表示，则需要加上一个1的维，也就是（2，1，1）；
    2. 然后平移旋转，我们可以构造一个旋转矩阵，然后将这个坐标和这个旋转矩阵相乘，完成旋转变换；
    3. 最后对于平移，我们同样可以构造一个平移矩阵，然后相乘就行，完成平移变换；

    想不起来的可以回顾一下这里：http://fjbq-blog.top/2023/12/30/GAMES%20101%20%E9%9A%8F%E7%AC%94/
*/

// 将角度转换为弧度
double DegToRad(double Deg)
{
    return Deg / 180.0 * M_PI;
}

void solve()
{
    // (2,1) 的点的齐次坐标表示（3 x 1 的矩阵）
    Eigen::Vector3f Point(2.0, 1.0, 1.0);

    // 旋转变换
    double Deg = 45.0;
    double Rad = DegToRad(Deg);

    Eigen::Matrix3f RotationMatrix;
    RotationMatrix  <<  cos(Rad), -sin(Rad), 0,
                        sin(Rad), cos(Rad), 0,
                        0, 0, 1;
    
    Point = RotationMatrix * Point;
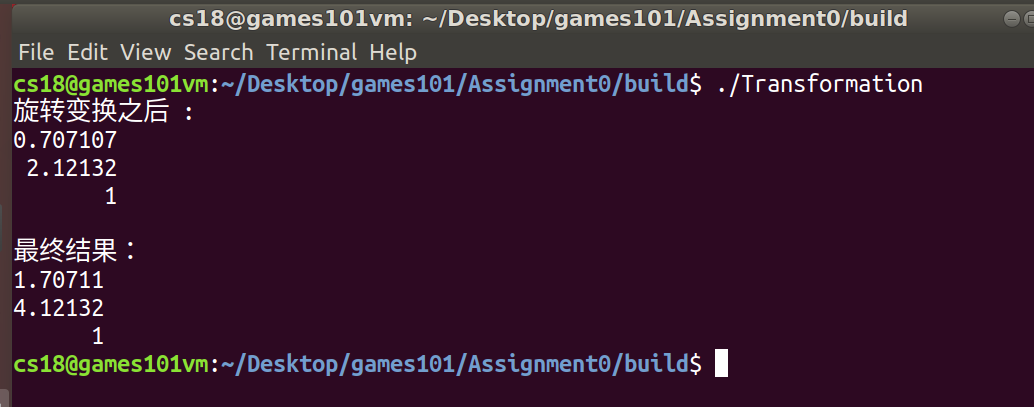
    cout << "旋转变换之后：\n" << Point << "\n\n";

    // 平移变换
    double tx = 1.0;
    double ty = 2.0;

    Eigen::Matrix3f TranslationMatrix;
    TranslationMatrix <<    1, 0, tx,
                            0, 1, ty,
                            0, 0, 1;

    Point = TranslationMatrix * Point;
    cout << "最终结果：\n" << Point <<'\n';
}

int main()
{
    solve();

    return 0;
}

结果：