HomeWork 4：Bézier 曲线

这个挺简单的，挺有意思的：

main.cpp

// 套公式求的 贝塞尔 曲线
void naive_bezier(const std::vector<cv::Point2f> &points, cv::Mat &window) 
{
    auto &p_0 = points[0];
    auto &p_1 = points[1];
    auto &p_2 = points[2];
    auto &p_3 = points[3];

    for (double t = 0.0; t <= 1.0; t += 0.001) 
    {
        auto point = std::pow(1 - t, 3) * p_0 + 3 * t * std::pow(1 - t, 2) * p_1 +
                 3 * std::pow(t, 2) * (1 - t) * p_2 + std::pow(t, 3) * p_3;

        window.at<cv::Vec3b>(point.y, point.x)[2] = 255;
    }
}

// 递归做法的贝塞尔曲线
cv::Point2f recursive_bezier(const std::vector<cv::Point2f> &control_points, float t) 
{
    // 只剩一个控制点的时候就能返回了
    if(control_points.size() == 1) return control_points[0];

    std::vector<cv::Point2f> temp_control_points;
    for(int i = 0; i < control_points.size()-1; i ++)
    {
        // 这个比较简单，看着图推一下就行
        cv::Point2f temp_point = control_points[i] - (control_points[i] - control_points[i+1]) * t;
        temp_control_points.push_back(temp_point);
    }

    return recursive_bezier(temp_control_points, t);
}

// 实现绘制 Bézier 曲线的功能（传进来一组控制点）
void bezier(const std::vector<cv::Point2f> &control_points, cv::Mat &window) 
{
    // 1000 个 t
    for(float t = 0; t <= 1; t += 0.001f)
    {
        cv::Point2f point = recursive_bezier(control_points, t);
        window.at<cv::Vec3b>(point.y, point.x)[1] = 255;
    }
}

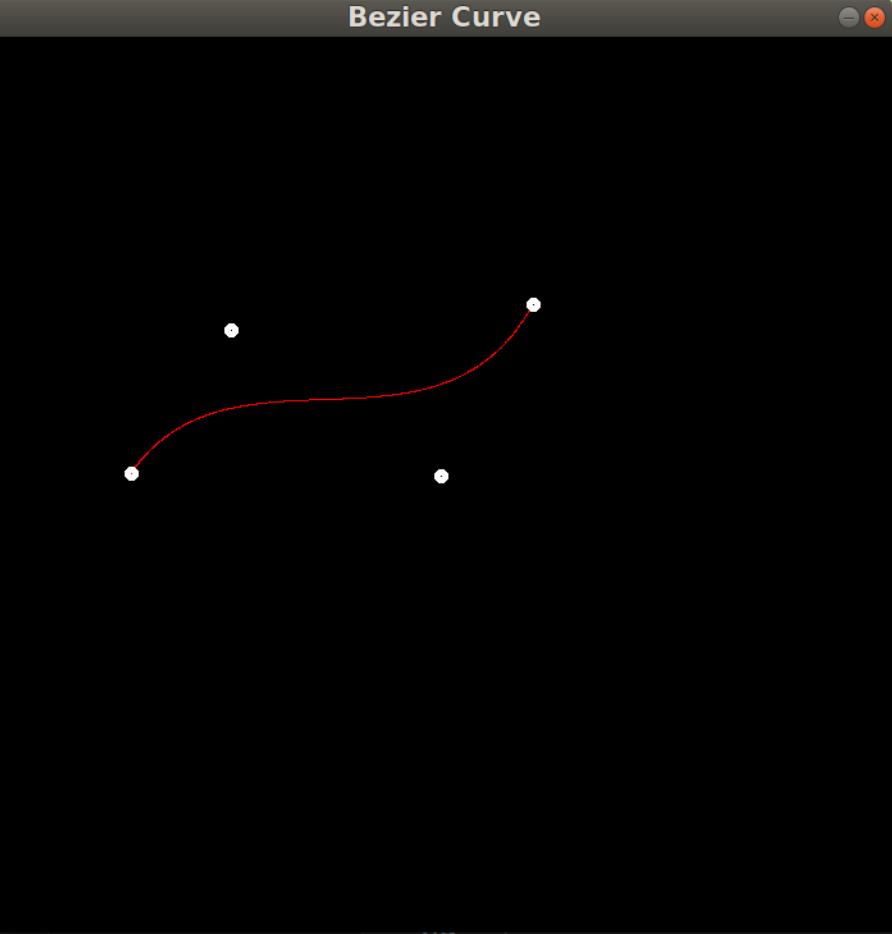
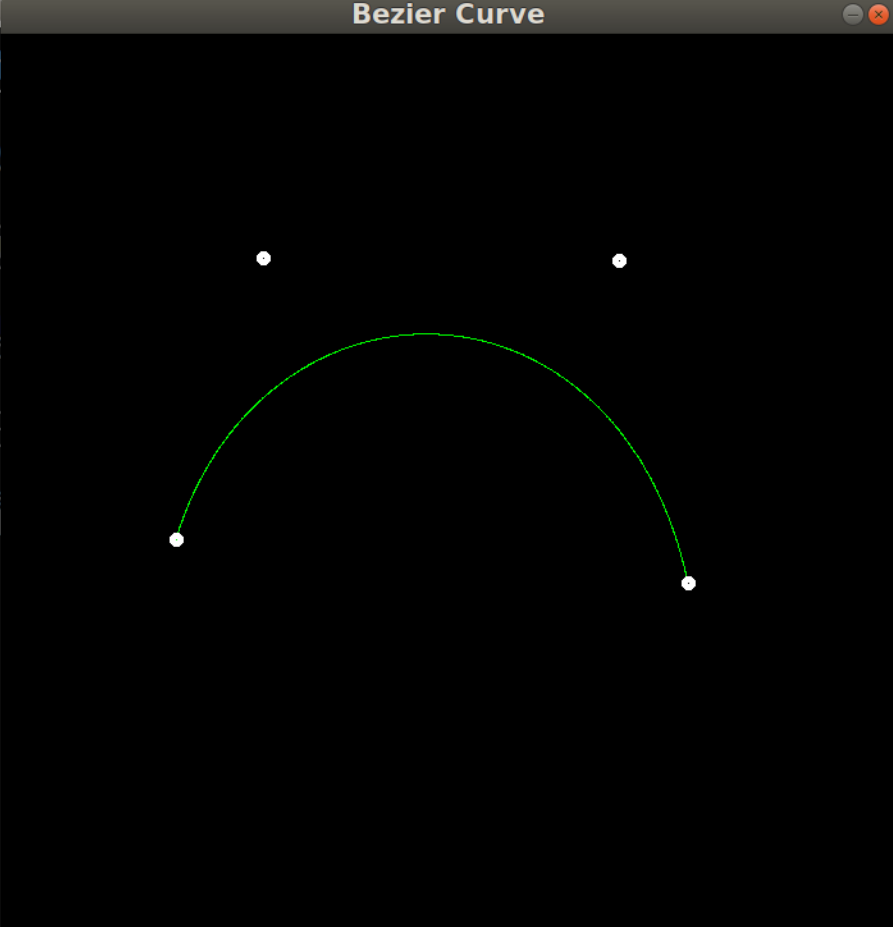
下面是贝塞尔曲线：
红色：公式
绿色：递归
黄色：两个同时调用的结果

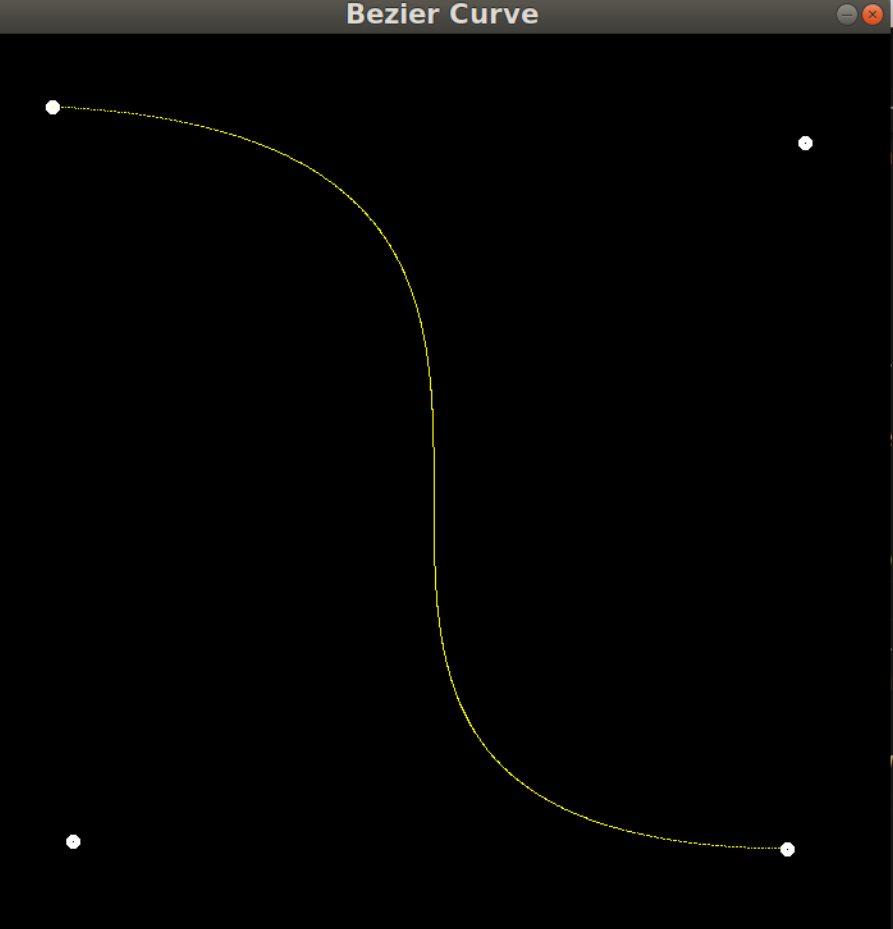
提高：（反走样）

/*
    做一下反走样
    https://zhuanlan.zhihu.com/p/464122963
*/
void bezier_2(const std::vector<cv::Point2f> &control_points, cv::Mat &window)
{
    for (float t = 0.0; t <= 1.0; t += 0.001)
    {
        cv::Point2f point = recursive_bezier(control_points, t);

        // 求距离点 point 最近的四个像素的像素交点中心（其实就是右下角的像素的起点）
        cv::Point2i p0;
        p0.x = point.x-std::floor(point.x) < 0.5 ? std::floor(point.x) : std::ceil(point.x);
        p0.y = point.y-std::floor(point.y) < 0.5 ? std::floor(point.y) : std::ceil(point.y);

        // 点 point 最近的四个像素点的起点
        std::vector<cv::Point2i> ps;
        ps.push_back(p0);
        ps.push_back(cv::Point2i(p0.x-1, p0.y));
        ps.push_back(cv::Point2i(p0.x, p0.y-1));
        ps.push_back(cv::Point2i(p0.x-1, p0.y-1));
        
        // 点 p 到相邻四个点的中心点的距离
        float sum_d = 0.0f;
        float max_d = sqrt(2);
        std::vector<float> ds = {};
        for (int i = 0; i < 4; i++) 
        {
            // 像素点的中心
            cv::Point2f cp(ps[i].x + 0.5f, ps[i].y + 0.5f);
            float d = max_d - std::sqrt(std::pow(point.x - cp.x, 2) + std::pow(point.y - cp.y, 2));
            ds.push_back(d);
            sum_d += d;
        }

        // 求一下加权的颜色直就行
        for (int i = 0; i < 4; i++) 
        {
            float k = ds[i] / sum_d;
            window.at<cv::Vec3b>(ps[i].y, ps[i].x)[1] = std::min(255.f, window.at<cv::Vec3b>(ps[i].y, ps[i].x)[1] + 255.f * k);
        }
    }
}

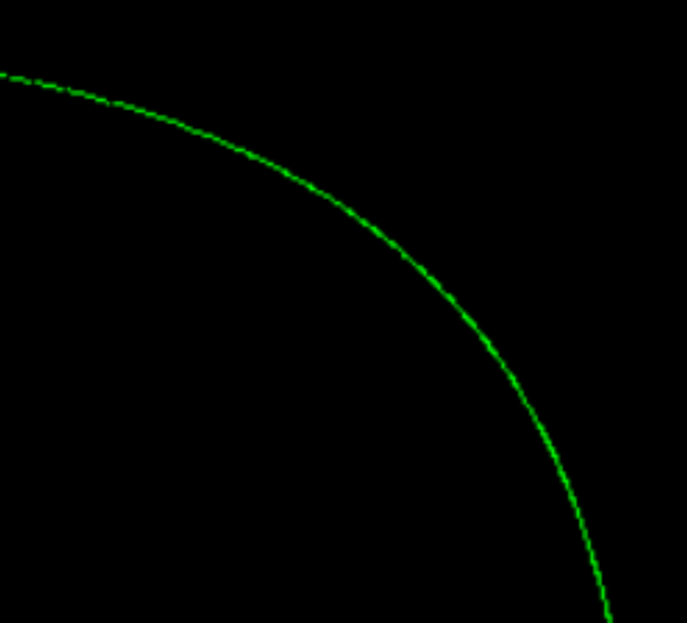
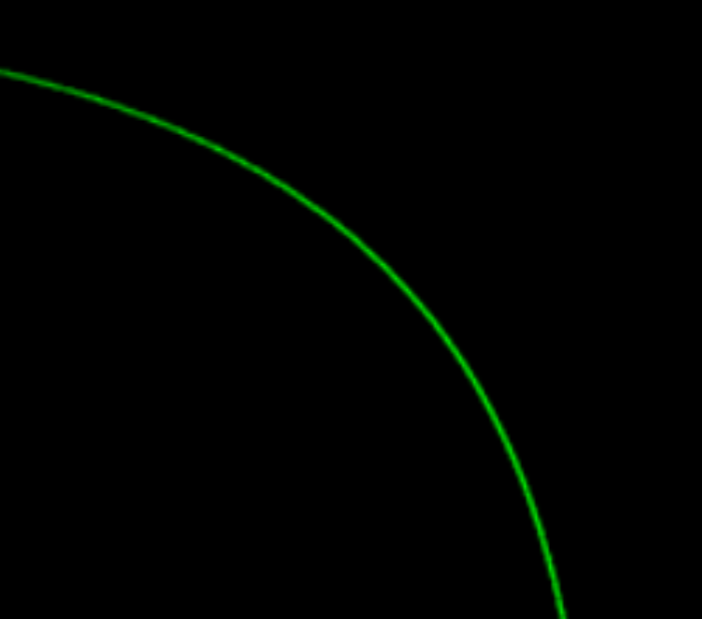
反走样对比，效果还是挺明显的：

FJBQ

【Games 101】HomeWork 4：Bézier 曲线

HomeWork 4：Bézier 曲线